Modelling HIV/AIDS epidemics in sub-Saharan Africa using seroprevalence data from antenatal clinics
Joshua A. Salomon1 & Christopher J.L. Murray2
OBJECTIVE: To improve the methodological basis for modelling the HIV/AIDS epidemics in adults in sub-Saharan Africa, with examples from Botswana, Central African Republic, Ethiopia, and Zimbabwe. Understanding the magnitude and trajectory of the HIV/AIDS epidemic is essential for planning and evaluating control strategies.
METHODS: Previous mathematical models were developed to estimate epidemic trends based on sentinel surveillance data from pregnant women. In this project, we have extended these models in order to take full advantage of the available data. We developed a maximum likelihood approach for the estimation of model parameters and used numerical simulation methods to compute uncertainty intervals around the estimates.
FINDINGS: In the four countries analysed, there were an estimated half a million new adult HIV infections in 1999 (range: 260 to 960 thousand), 4.7 million prevalent infections (range: 3.0 to 6.6 million), and 370 thousand adult deaths from AIDS (range: 266 to 492 thousand).
CONCLUSION: While this project addresses some of the limitations of previous modelling efforts, an important research agenda remains, including the need to clarify the relationship between sentinel data from pregnant women and the epidemiology of HIV and AIDS in the general population.
Keywords Acquired immunodeficiency syndrome/epidemiology; HIV infections/epidemiology; HIV seroprevalence/ trends; Models, Statistical; Sentinel surveillance; Africa South of the Sahara (source: MeSH).
Mots clés SIDA/épidémiologie; HIV, Infection/épidémiologie; HIV séroprévalence/orientations; Modèle statistique; Surveillance par système sentinelle; Afrique subsaharienne (source: INSERM).
Palabras clave Síndrome de inmunodeficiencia adquirida/epidemiología; Infecciones por VIH/epidemiología; Seroprevalencia de VIH/tendencias; Modelos estadísticos; Vigilancia de guardia; Africa subsahariana (fuente: BIREME).
Introduction
In the two decades since the first cases of AIDS were identified, HIV/AIDS has emerged as one of the leading challenges for global public health. Particularly in sub-Saharan Africa, where the majority of HIV and AIDS cases are concentrated, the epidemic continues to take an extraordinary human toll. To plan and evaluate control strategies effectively and to prepare for vaccine efficacy trials, it is critical to estimate the magnitude and trajectory of the HIV/AIDS epidemic. Trade-offs between alternative interventions and policies must be based on the best possible information about current levels and trends in the epidemic.
Unfortunately, population-based epidemiological data for sub-Saharan Africa are extremely limited. Incidence data are rare because direct measurement is difficult, and because cohort studies are expensive and require long follow-up periods; AIDS notification data capture only a fraction of new AIDS cases and are subject to reporting delays. Information on AIDS-attributable mortality is also essential to assess the impact of the epidemic, but vital registration systems have extremely limited coverage in most of sub-Saharan Africa. Other population-based mortality data, while increasingly available for children through the Demographic and Health Surveys (1), are uncommon for adults.
Seroprevalence data
The most widely available epidemiological data on HIV/AIDS in Africa are seroprevalence data. Although population-based prevalence surveys would be the most useful, they have been undertaken in only a small number of locations (212). By contrast, sentinel surveillance systems, which monitor the prevalence of HIV infection in specific subpopulations, have been established in countries throughout the region, and data are available for a range of different population groups, including commercial sex workers, injecting drug users, blood donors, and pregnant women attending antenatal clinics. It is believed that the antenatal clinic data most closely approximate prevalence levels in the adult population, although the relationship between prevalence among clinic attendees and that of the general population remains uncertain (13).
The need for models
Given the need to understand better the levels and trends of the HIV epidemic, and the limited information on which to base these estimates, mathematical models can make a valuable contribution. The goal of any modelling exercise is to extract as much information as possible from available data and provide an accurate representation of both the knowledge and uncertainty about the epidemic. A number of different models of HIV and AIDS have been developed, ranging from simple extrapolations of past curves (14) to complex transmission models (1518).
A major tradition in modelling HIV/AIDS epidemics has been to use backcalculation, or backprojection, techniques. These techniques produce statistical solutions to convolution equations that relate the number of AIDS diagnoses over time to past trends in HIV infection, and to the distribution of the HIV incubation period. The models were introduced more than a decade ago (19, 20) and have been applied in many settings (2128), almost exclusively in industrialized countries where AIDS notification is imperfect, but considerably more complete than in most developing countries. Several studies have tried to account for the effects of different sources of uncertainty on the trajectory of the epidemic, including the length of reporting delays, the distribution of HIV incubation times (29), and the effects of treatment and other issues (24, 30).
Epimodel
Traditional backcalculation methods cannot be used to model HIV epidemics in developing countries due to the paucity of reliable information on the incidence of AIDS. A modified framework was therefore developed by WHO to reconstruct HIV incidence curves and develop short-term projections, based on the prevalence of HIV infection, rather than on AIDS notifications. The model developed by WHO was formalized in a software programme called Epimodel (31). Epimodel uses an input estimate of point prevalence in a reference year, combined with assumptions about HIV/AIDS progression rates and the start year of the epidemic, to reconstruct incidence curves from the beginning of the epidemic. Because there could be an infinite number of incidence curves consistent with a particular start year and point prevalence estimate, Epimodel imposes further structure on the estimation by assuming that the HIV infection rate follows a parametric curve over time based on the gamma distribution. Both the shape of the curve and the position on the curve in the anchor year are required inputs. Epimodel may thus be considered a deterministic variant of the original backcalculation models.
Epimodel was used to produce a series of estimates by the former WHO Global Programme on AIDS, and by the collaborative efforts of WHO and the Joint United Nations Programme on HIV/AIDS (UNAIDS). Several sets of regional estimates have been developed since 1989, based on the estimated number of HIV-infected individuals in each region (3234). The first country-level estimates of the epidemic were also produced with Epimodel (35), using country estimates of infection prevalence for 1994 (36) and revisions of these estimates for 1997. Epimodel was also used in the most recent round of WHO/UNAIDS country estimates for sub-Saharan Africa, using prevalence data from antenatal clinics as the starting point (37).
Given the accumulation of surveillance data over the last 10 years, it is worth revisiting some of the strong restrictions in Epimodel that were necessitated by the dearth of data at the time of its development. In particular, it is important to reconsider the reliance on expert judgment, rather than on analytical strategies that use the full set of available data. In this paper, we adapted the statistical tools developed in the original backcalculation work to the problem of modelling epidemics in developing countries. This is especially important given the need to characterize the uncertainty around the HIV epidemics in sub-Saharan Africa. For this study, some of the basic assumptions used in Epimodel were preserved, but the deterministic structure imposed on the curve-fitting procedure has been relaxed. Using a maximum likelihood approach, it was possible to use all of the available data for the curve-fitting exercise, as well as to represent some of the uncertainty in the estimates. The two main goals were to improve the methodological basis for modelling the HIV/AIDS epidemics in sub-Saharan Africa, and to develop estimates of incidence, prevalence, and mortality over time that included ranges of uncertainty. Although we focused on adult populations in sub-Saharan Africa, the epidemiology of HIV/AIDS in children is also important, but was outside the scope of this study.
Methods
Data Sources
The objective of the modelling exercise was to estimate trends in HIV/AIDS incidence and mortality, using sentinel surveillance data on HIV seroprevalence among pregnant women attending antenatal clinics. The sentinel surveillance programme is based on anonymous, unlinked testing in a selection of clinics within a country, with each clinic reporting the annual proportion of attendees that tested positive for HIV infection. The United States Bureau of the Census has compiled these data since 1987 (38) and they are presented by UNAIDS and WHO in the form of Epidemiological fact sheets for each country (39). Sentinel data from antenatal clinics are available for nearly every African country for at least one year, but there is considerable variation in the number of clinics that report each year.
The Epidemiological fact sheets divide sites into two categories: major urban areas and outside major urban areas. For a number of countries, there were insufficient data from both urban and non-urban areas to estimate all model parameters. We therefore selected four countries with sufficient data for both types of areas to reflect a range of surveillance coverage levels: Botswana, Central African Republic, Ethiopia, and Zimbabwe. Table 1 summarizes the seroprevalence data from these four countries. For this analysis it was assumed that seroprevalence in the general population may be inferred from data in the sentinel populations, but this assumption is examined further below.
Backcalculation equation
As in Epimodel, the model presented here adapted the original backcalculation framework by focusing on HIV seroprevalence data, rather than AIDS notifications. The foundation of the model was the relationship between prevalence, incidence, and survivorship over time for infected individuals. Defining t = 0 as the first year of the epidemic, the number of HIV-infected individuals at time t is equal to the total number of individuals who were infected before time t and are still alive at time t:

where P(t) is the prevalence of infected people at time t expressed as an absolute number, I(s) is the number of new infections occurring between time s and (s+1), and F(t) is the probability that an individual will survive at least t years after being infected. Half a year is subtracted from the duration in the survivorship function, under the assumption that the average moment of infection within a given time period is the midpoint of that period. For example, prevalence at year 10 in the epidemic would include those individuals infected during the ninth year who have endured an average of 0.5 years mortality risk, plus those individuals infected during the eighth year who have endured an average of 1.5 years of mortality risk, and so on.
Eq. 1 was defined in terms of absolute numbers of incident and prevalent infections. A slight modification was necessary to express the relationship in proportions rather than absolute numbers. In the simplest case, where the population size does not change over time, Eq. 1 translated directly to proportions, as both sides of the equation may be divided by the population number at time t, Pop(t):

In a stable population, Pop(t) = Pop(s) for all s, which leads to:
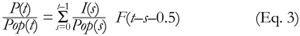
or, equivalently:
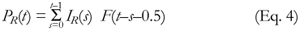
where PR(t) is the proportion of the population who have prevalent infections at time t, and IR(s) is the incidence of new infections between time s and (s+1), expressed as a proportion of the population at time s.
If the population size changes over time, an additional factor is required to capture this change:
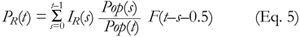
The statistical model
Based on the relationship described in Eq. 5, the backcalculation approach uses prevalence data at different time points, combined with survivorship assumptions, to reconstruct past trends in incidence, expressed as the vector IR(s) for s = (0, 1, 2, ..., t). Given that the earliest observed prevalence in the data set is from 1986, identification of all elements of IR(s) would be impossible without imposing some structure on the shape of the infection curve. Specification of an incidence curve defined by a minimal number of parameters serves both to reduce the dimension of the problem and to allow estimation of trends prior to the first observed data point. Even if the prevalence data extended as far back as the beginning of the epidemic, additional structure on the shape of the infection curve would be useful in constraining improbable oscillations in estimates of incidence over time. Proponents of the backcalculation approach have selected various parametric forms for the incidence curve, based on empirical observation of epidemics and insights from dynamic mathematical models. Details of the functional forms for incidence and the survivorship assumptions used in this paper are described below. For any specification, a set of values on all of the parameters will define a unique set of incidence and prevalence curves over time according to Eq. 5. The analytical objective is to estimate the set of parameter values that are most likely to have produced the observed prevalence data.
To estimate the parameters, the observed data on prevalence were related to an underlying stochastic model. One simple model might assume that the set of prevalence observations from different sites in a particular year was drawn from a normal distribution with an expected value defined by Eq. 5, conditional on a specified incidence and survivorship. In this model, the task would be to estimate the set of parameter values that define an average national infection curve and survivorship function, as well as an additional parameter indicating the variance in prevalence across different sites in a given year. More complicated models may be warranted if additional information on individual sites could be used to define site-specific prevalence distributions, with expected values related to these additional variables. If the sample sizes in each site were known, it would also be possible to account for sampling variation within each site, in addition to the variability across sites.
In the data set used here, the only additional information that distinguished sites was their location either inside or outside major urban areas. Evidence from epidemiological studies suggests that epidemics tend to originate in highly populated areas, such as major cities and trading centres, and then radiate outward to less populated areas (10). We have therefore allowed for distinct but related epidemics in urban populations and non-urban populations within each country. It was assumed that observations from urban sites were drawn from one distribution, while observations in non-urban sites were drawn from a separate distribution, although the mean values of the two distributions were related through the parametric models for incidence, as described below.
Parameter specification
Parametric forms for IR(.) and F(.) were developed using Epimodel assumptions as points of reference.
The general model is presented first, followed by a description of the differences between the urban and non-urban models. The shape of the incidence curve over time was based on the shape of a gamma density function, chosen for its convenience and flexible form, rather than for its implications in terms of probability:

The use of a density function as the basis for IR(s) required two modifications before the function could serve as a plausible model of trends in incidence. Firstly, g(s) was multiplied by an additional scalar, g, to allow the entire curve to be adjusted to an appropriate level for incidence rates. Secondly, because the density function declined rapidly to zero after its mode, it was likely to give a poor representation of an epidemic after it peaks. Insights from dynamic transmission models (16), and evidence from the advanced epidemic in Uganda (5, 40), both suggested that incidence would be more likely to approach a stable equilibrium level above zero. A parameter, q, determining the equilibrium incidence level in relation to the peak incidence level, was thus incorporated in the model. After the mode, which occurred at b(a1), incidence during year s was computed as a weighted average of gg(s) and the modal value.ª The weight on the modal value was q, constrained in this study to be between 0.25 and 0.75, based on the limited evidence available. Including these two modifications, the level and trajectory of an incidence curve was determined by the values of four parameters (see Eq. 7 below). This functional form offered considerable flexibility in defining a wide range of different possible curves.

The incidence curve for urban populations may differ from that for non-urban populations in three ways: firstly, g may be different i.e. the overall level of the epidemic may be higher or lower; secondly, q may be different i.e. the epidemic may settle to a different equilibrium level; and thirdly the epidemic may unfold over a faster or slower time course. This was modelled by multiplying every occurrence of s in Eq. 7 by a scalar parameter q. The scalar is also applied to both occurrences of b(a1) in the second line of Eq. 7. If q>1, then the non-urban epidemic rises and falls at a more accelerated pace than the urban epidemic; conversely, q<1 implies a slower epidemic outside of urban areas. Thus, the urban and non-urban incidence curves in each country shared certain common parameters, but differed in others, and a total of seven parameters defined the urban and non-urban curves within a country. Urban incidence was a function of a, b, gU, and qU, while non-urban incidence was a function of a, b, gN, qN, and q.
The time from infection to death was assumed to follow a Weibull distribution. Consequently, the probability that an individual will survive at least t years after infection, F(t), is summarized by the following two-parameter function:

The Weibull distribution has been used frequently to describe the distribution of AIDS incubation times (19, 20, 25, 26). In industrialized countries, the advent of highly active antiretroviral therapy (HAART) has undoubtedly altered the survivorship function, but the uptake of HAART in Africa has been minimal to date. Nevertheless, uncertainty around the survivorship function remains an important issue to be addressed in future work. For this exercise, data limitations demanded a parsimonious model, so the Weibull parameters were fixed at k = 0.021 and y = 1.6. These parameters were chosen to match the baseline assumptions in Epimodel, with a median time from HIV infection to death of approximately 9 years.
To further simplify Eq. 5, it was assumed that population growth occurred at a constant rate in each country during the years spanned by the epidemic. Although the demographic impact of the HIV epidemic has probably altered the accuracy of this assumption, the implications of this error on the model results are negligible. Assuming that the population is growing at a constant rate, r, then Pop(s) = Pop(t)e-r(t-s) for s = (0, 1,..., t). Thus, the sequence of ratios Pop(s)/Pop(t) for s = (0, 1, ..., t) may be summarized simply as e-r(t-s) in Eq. 5, which reduces the information requirement from the full sequence of populations over time to a single constant. An average growth rate of 3% was used in this exercise and the results were insensitive to changes in this assumption.
Estimation of parameters
For each country, the parameters for urban and non-urban epidemics were estimated simultaneously, allowing for correlations between the various parameters. The final model included eight unknown parameters: the seven incidence parameters and one additional parameter that indicated variance across sites in each year within the urban or non-urban categories.
Maximum likelihood estimation (MLE) was used to identify the vector of parameter values that most likely produced the full set of observed prevalence data in urban and non-urban sites for each country. The MLE parameter values were translated into maximum likelihood estimates of incidence and prevalence over time. National estimates were calculated as the average of the urban and non-urban estimates, weighted by the respective populations. Using a similar relationship as that described in Eq. 5, it was also possible to compute trends in population mortality over time, based on a specified incidence curve and survivorship function:
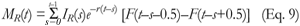
where MR(t) is the proportion of the population at time t that will die with HIV infection between time t and time (t+1); IR(s) and F(t) are defined as before. For example, deaths occurring in HIV-positive individuals during the tenth year of the epidemic will include those people who were infected during year 0 and have survived for more than 9.5 but less than 10.5 years after being infected, plus those who were infected during year 1 and survived for more than 8.5 but less than 9.5 years after being infected, and so on.
Eq. 5 and Eq. 9 thus allowed a set of parameters describing incidence and survivorship to be translated into curves that represented population prevalence and mortality over time.
Uncertainty analysis
The use of a likelihood approach allowed estimation not only of the MLE values for incidence, prevalence, and mortality, but also a measurement of uncertainty around these estimates. Given the structure of the model, there were many different epidemic curves that could have provided an acceptable fit to the available data. The range of different past trends that might plausibly have produced the observed data points were estimated through the likelihood approach and were represented by upper and lower bounds on the quantities of interest.
Numerical simulation methods were used to identify a range of plausible values for the unknown parameters. In each country, 20 000 sets of candidate parameter vectors were generated by sampling from a triangular distribution around each parameter. Each distribution was defined based on the parameter estimate and standard error produced by the MLE procedure, with a peak at the MLE value and a range spanning two standard errors above and below the MLE value, subject to the logical constraints on each parameter e.g. by definition, g must be greater than zero. For each candidate vector of parameter values, a likelihood ratio statistic was calculated as twice the difference between the maximum log likelihood and the log likelihood under the candidate values. Based on a c² approximation with 8 degrees of freedom, the likelihood interval, chosen to correspond to an approximate 95% confidence interval, was defined to include the subset of parameter vectors for which the likelihood ratio statistic was less than 15.51.
For the MLE parameter values and each of the parameter vectors in the likelihood interval, national estimates for HIV incidence, HIV prevalence, and AIDS mortality were calculated as the average of the urban and non-urban values, weighted by the size of the respective populations. For any given year, ranges around incidence, prevalence, and mortality were defined by the highest and lowest values for these measures computed from the subset of parameter vectors in the likelihood interval.
The bounds produced in this analysis reflect uncertainty around the parameter estimates, but do not capture other sources of uncertainty relating to the specification of the model (model uncertainty) and the data to which the model is fit (sampling error and measurement error).
Results
Fig. 1 presents a comparison between the model results for prevalence in each of the four countries and the observed data on prevalence in pregnant women from the sentinel surveillance sites. In Botswana and Ethiopia, HIV seroprevalence was systematically higher in urban areas, when compared to levels outside urban areas. However, data from the Central African Republic indicate that seroprevalence levels in non-urban areas may rise later but then more rapidly than levels in urban areas. (In the model results for the Central African Republic, one relatively high prevalence observation in a non-urban site in 1986 appears to have dampened this effect.) In Zimbabwe, recent trends were unclear, as was the relationship between urban and non-urban epidemics, since there were few urban sites and only one observation since 1995. In none of the countries was there conclusive evidence that prevalence levels have peaked, although evidence from Botswana and Ethiopia were suggestive of recent peaks. In the Central African Republic prevalence rates rose steadily through 1996, when the last observations were made.
Using the maximum likelihood parameter estimates and the range of parameter values in the likelihood interval, estimates of incidence, prevalence, and mortality over time were developed, together with upper and lower bounds on these estimates (Figs 24). Fig. 2 suggests that incidence rates are currently declining in Botswana, Ethiopia, and Zimbabwe, but may still be rising in the Central African Republic. The bounds indicate the uncertainty around the range of past trends that are consistent with observed prevalence data in each country. In relative terms, the greatest degree of uncertainty occurs in Ethiopia, where there is considerable ambiguity about the year in which incidence may have peaked, as well as more than a fourfold difference between the upper and lower estimates of incidence in the year 2000. The difference between upper and lower estimates for 2000 is approximately threefold in Zimbabwe and smaller in Botswana and the Central African Republic. Generally, the level of uncertainty is greatest for the most recent estimates, as prevalence data provide more information about levels and trends in incidence several years before the date of reporting than those that are nearer in time.
Fig. 3 presents the results for prevalence estimates. Again, the greatest degree of uncertainty appears in Ethiopia, following directly from the uncertainty in the incidence estimates. Overall, the levels of uncertainty around prevalence are smaller than those around incidence, as the models are fit to the prevalence data and thereby constrained to match observed trends as closely as possible. Where there are more data points that trace a relatively smooth trajectory over time, as in Botswana, the bounds around prevalence are relatively tight.
Mortality estimates for the four countries are shown in Fig. 4. Because of the long incubation period, trends in mortality rates tend to lag approximately 10 years behind trends in incidence. Thus, if incidence in Botswana peaked around 1994, then mortality is expected to continue to increase for several years into the next decade. A given level of uncertainty around incidence translates into a smaller level of uncertainty around mortality in each year, conditional on fixed values for the progression distribution. This is because the incident cases from a particular year will follow some distribution in terms of the time from infection to death, so that changes in incidence over a short period tend to be smoothed out over longer periods in terms of mortality.
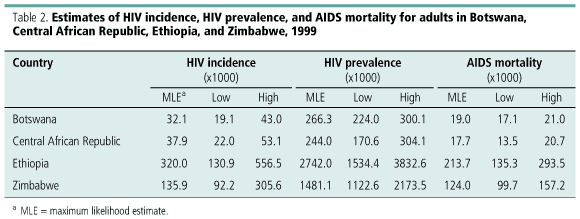
The estimates and ranges for incidence, prevalence, and mortality in each country in 1999 are summarized in Table 2. The rates in Figs 24 have been translated into absolute numbers by applying national population estimates. Of the four countries, Ethiopia has the lowest rates but the largest population, so the absolute size of the epidemic is notably larger than in the other three countries. In the four countries, there were an estimated half a million new adult HIV infections in 1999 (range: 260 to 960 thousand), with an estimated prevalence of 4.7 million cases (range: 3.0 to 6.6 million). It is estimated that more than 370 thousand adults died from AIDS in these countries in 1999 (range: 266 to 492 thousand).
Discussion
We have presented a method for modifying current models of the HIV epidemics in sub-Saharan Africa to take advantage of all available data and reflect the uncertainty in estimates produced by fitting models to a small number of data points. It is important to note that this method captured one important component of uncertainty, but excluded others. Specifically, the maximum likelihood approach reflected the fact that there were a range of different past trends that might have fitted the observed data points on prevalence, but omitted uncertainty as to the correct model specification, the incubation distribution, and, perhaps most importantly, the generalizability of sentinel surveillance data among pregnant women attending antenatal clinics.
This study addressed one of the major criticisms of Epimodel, namely that the unmodified gamma distribution gives a poor representation of the decline in an epidemic after its peak. The gamma function was modified to allow the epidemic to settle into an equilibrium at some level above zero. Nevertheless, limited evidence is available on precise equilibrium levels in real epidemics, so further improvements may be possible if new insights are derived from transmission models or, preferably, from direct measures of incidence in populations. It is also important to recognize that reductions in risk behaviour following interventions or other changes may have important benefits that were not well captured in the parametric curve used in this model. The model for the incubation period distribution was another source of uncertainty that might be addressed in future work. In this area, while statistical estimation may be informative, the results from ongoing natural history cohort studies (4144) will be most critical.
Extrapolation of model data
One of the key assumptions in the model was that sentinel data from pregnant women may be extrapolated to the entire population. There have been a handful of studies that have addressed the question of whether prevalence rates in antenatal clinic sites were representative of the population prevalence rates. This question can be considered on three levels: firstly, do prevalence rates in antenatal clinic sites represent the general population rates in these areas among women of the same age as clinic attendees? Secondly, do prevalence rates among women in these age groups represent the overall prevalence rates in the adult population in these areas? Thirdly, do prevalence rates in the sentinel areas represent national prevalence rates? The answers to these questions are likely to vary widely across different settings because of the stage of the epidemic, along with a host of other factors. The few studies that have addressed these questions, however, provide valuable reference points for further research.
On the first question, there is evidence that women attending antenatal clinics may have similar or lower prevalence rates than women of the same ages in the general population of these areas. A study in Zambia (2) found that age-adjusted prevalence rates in women attending antenatal clinics were 24.427.5% between 199496, compared to 31.2% in the general population in urban areas; and were 12.5% compared to 17.4% in rural areas. Studies in Mwanza region, United Republic of Tanzania (12, 45) found that women aged up to 35 years attending antenatal clinics had lower prevalence rates than women in the population of the same ages, although rates among women older than 35 years were higher in the antenatal clinic group. Another study in Kagera region, United Republic of Tanzania (11) found similar results, with an overall age-adjusted prevalence of 29.4% in the general population sample, compared to 22.4% in the antenatal clinic sample.
On the second question, one of the principal concerns is whether prevalence levels are different among men and women. Berkley et al. (46) found in three studies in Uganda that women had higher prevalence rates than men, with female-to-male prevalence ratios of 1.42 in semi-rural communities, 1.56 in rural Rakai district, and 1.31 in a national serosurvey. Standardizing on the estimated age and sex distribution in the general population, the ratios were 1.34, 1.41, and 1.19, respectively. Likewise, the Kagera study found age-adjusted prevalence rates of 29.4% among females compared to 16.7% among males. In the Zambia study cited above, age-adjusted prevalence rates were comparable in males and females in rural areas (15.4% in males and 17.4% in females) but significantly lower among males than females in urban areas (20.9% compared to 31.2%). The same findings were reported in Mwanza (45), with lower rates for males than females in urban areas (9% compared to 15%) and similar rates in non-urban areas (3% compared to 4%).
Perhaps the most critical question is whether the sentinel areas provide an adequate representation of the range of prevalence levels at the national level. Studies in various countries have found significant differences across different types of areas, reflecting important distinctions that may be missed by a broad classification of sites as urban or non-urban. For example, one study in Arusha region, United Republic of Tanzania (10) compared prevalence rates in high- and low-socioeconomic status urban areas, in semi-urban areas, and in rural areas, and found that prevalence rates among women were 13.3%, 7.4%, 3.4%, and 1.1%, respectively, with corresponding rates among men of 5.3%, 1.0%, 0%, and 2.1%, respectively. If the selection of sentinel areas in a country does not match the population distribution across urban, peri-urban, and rural areas, this may be an important source of selection bias in national prevalence estimates that are based on sentinel surveillance systems.
The problem of extrapolating from a collection of individual sites to a national prevalence level would be greatly facilitated by additional information on the different sites. For example, information about the catchment areas of particular hospitals would allow different sites to be weighted according to the proportion of the population covered by each site. Additionally, simple geographical analyses may provide useful information on which sites are likely to have related epidemics due to proximity. If more information on the sites could be incorporated formally into epidemic models, the validity of the results would probably improve dramatically.
Future approaches
As work on modelling the HIV/AIDS epidemic proceeds, it is crucial to undertake rigorous validation exercises on the modelling methods and results. One approach would be to compare the model-based mortality estimates to demographic information on AIDS-related mortality in a country, although the challenge of finding adequate population-based mortality data in sub-Saharan Africa remains daunting. Preliminary work to validate the model results presented here, using a series of mortality studies from Zimbabwe, suggests that these models may have overestimated the level of the epidemic in Zimbabwe, but the effects of potential biases in the mortality data remain to be assessed and may affect this conclusion. The identification of valid data sources for demographic estimates of HIV/AIDS-attributable mortality must be a priority in this area.
In spite of the level of uncertainty that remains around the epidemic, it is clear that the HIV/AIDS epidemic is a major public health challenge that demands an effective policy response. We hope that this paper will contribute towards continuing efforts to improve understanding of the epidemic as an important step in planning and evaluating this response. 
Acknowledgements
The authors gratefully acknowledge valuable input from Emmanuela Gakidou, Neff Walker, Bernhard Schwartlander, Gary King, Alan Lopez, Rafael Lozano, Omar Ahmad, Grace Lee, Sue Goldie, Milt Weinstein, Jim Hammitt, and two anonymous reviewers.
Conflicts of interest: none declared.
Résumé
Modélisation des épidémies de VIH/SIDA en Afrique subsaharienne à partir des données de séroprévalence des dispensaires de soins anténatals
OBJECTIF: Améliorer les bases méthodologiques de la modélisation de lépidémie de VIH/SIDA chez ladulte en Afrique subsaharienne, avec des exemples provenant du Botswana, dEthiopie, de République centrafricaine et du Zimbabwe. Il est indispensable de connaître lampleur et la trajectoire de lépidémie de VIH/SIDA pour planifier et évaluer les stratégies de lutte.
MÉTHODS: Des modèles mathématiques ont déjà été élaborés pour estimer les tendances épidémiques daprès les données de la surveillance sentinelle des femmes enceintes. Dans le présent projet, nous avons étendu ces modèles de façon à pouvoir exploiter au maximum les données disponibles. Nous avons mis au point une approche selon la vraisemblance maximale pour lestimation des paramètres du modèle et fait appel à une simulation numérique pour calculer les intervalles dincertitude attachés aux estimations.
RÉSULTATS: Dans les quatre pays dont nous avons analysé les données, les estimations étaient de 500 000 nouvelles infections par le VIH en 1999 chez ladulte (intervalle : 260 000-960 000), 4,7 millions dinfections établies (intervalle : 3,0-6,6 millions), et 370 000 décès dus au SIDA chez ladulte (intervalle : 266 000-492 000).
CONCLUSION: Ce projet permet de répondre à certaines limitations des modèles existants, mais il reste dimportantes questions à résoudre, et il est en particulier nécessaire délucider la relation entre les données sentinelles sur les femmes enceintes et lépidémiologie du VIH et du SIDA dans la population générale.
Resumen
Modelización de la epidemia de VIH/SIDA en el África subsahariana a partir de los datos de seroprevalencia de dispensarios de atención prenatal
OBJETIVO: Mejorar la base metodológica para modelizar la epidemia de VIH/SIDA en la población adulta en el África subsahariana, con ejemplos de Botswana, la República Centroafricana, Etiopía y Zimbabwe. El conocimiento de las dimensiones y las tendencias de la epidemia de VIH/SIDA es fundamental para planificar y evaluar las estrategias de lucha.
MÉTODOS: Los modelos matemáticos previos se desarrollaron para estimar las tendencias de la epidemia a partir de los datos de vigilancia centinela obtenidos con mujeres embarazadas. En este proyecto hemos ampliado esos modelos para explotar al máximo los datos disponibles. Desarrollamos un método de máxima verosimilitud para calcular los parámetros del modelo y empleamos métodos de simulación numérica para calcular los intervalos de incertidumbre en torno a esas estimaciones.
RESULTADOS: En los cuatro países analizados, las estimaciones arrojaron la cifra de medio millón de nuevas infecciones de adultos por el VIH en 1999 (intervalo: 260 000960 000), una prevalencia de 4,7 millones de infecciones (intervalo: 3,06,6 millones) y 370 000 defunciones de adultos por SIDA (intervalo: 266 000492 000).
CONCLUSIÓN: Si bien en este proyecto se abordan algunas de las limitaciones demodelizaciones anteriores, éste sigue siendo un campo de investigación importante, en el que destaca la necesidad de esclarecer la relación entre los datos centinela obtenidos a partir de las mujeres embarazadas y la epidemiología del VIH y el SIDA en la población general.
References
1. Demographic and Health Surveys. Calverton, MD, Macro International, 20001 (Internet communication, 15 June 2001 at http://www.measuredhs.com/).
2. Fylkesnes K et al. Studying dynamics of the HIV epidemic: population-based data compared with sentinel surveillance in Zambia. AIDS, 1998, 12 (10): 12271234.
3. Serwadda D et al. HIV risk factors in three geographic strata of rural Rakai District, Uganda. AIDS, 1992, 6 (9): 983989.
4. Sewankambo NK et al. Demographic impact of HIV infection in rural Rakai District, Uganda: results of a population-based cohort study. AIDS, 1994, 8 (12): 17071713.
5. Wawer MJ et al. Trends in HIV-1 prevalence may not reflect trends in incidence in mature epidemics: data from the Rakai populationbased cohort, Uganda. AIDS, 1997, 11 (8): 10231030.
6. Wawer MJ et al. A randomized, community trial of intensive sexually transmitted disease control for AIDS prevention, Rakai, Uganda. AIDS, 1998, 12 (10): 12111225.
7. Shao J et al. Population-based study of HIV-1 infection in 4,086 subjects in northwest Tanzania. Journal of Acquired Immune Deficiency Syndromes, 1994, 7 (4): 397402.
8. Grosskurth H et al. A community trial of the impact of improved sexually transmitted disease treatment on the HIV epidemic in rural Tanzania: 2. Baseline survey results. AIDS, 1995, 9 (8): 927934.
9. Mulder DW et al. HIV-1 incidence and HIV-1-associated mortality in a rural Ugandan population cohort. AIDS, 1994, 8 (1): 8792.
10. Mnyika KS et al. Prevalence of HIV-1 infection in urban, semi-urban and rural areas in Arusha region, Tanzania. AIDS, 1994, 8 (10): 14771481.
11. Kwesigabo G, Killewo JZJ, Sandström A. Sentinel surveillance and cross sectional survey on HIV infection prevalence: a comparative study. East African Medical Journal, 1996, 73 (5): 298302.
12. Kigadye R-M et al. Sentinel surveillance for HIV-1 among pregnant women in a developing country: 3 years experience and comparison with a population serosurvey. AIDS, 1993, 7 (6): 849855.
13. Boisson E et al. Interpreting HIV seroprevalence data from pregnant women. Journal of Acquired Immune Deficiency Syndromes and Human Retrovirology, 1996, 13 (5): 434439.
14. Healy MRJ, Tillett HE. Short-term extrapolation of the AIDS epidemic. Journal of the Royal Statistical Society (A), 1988, 151 (1): 5065.
15. Anderson RM et al. The spread of HIV-1 in Africa: sexual contact patterns and the predicted demographic impact of AIDS. Nature, 1991, 352: 581589.
16. Bongaarts J. A model of the spread of HIV infection and the demographic impact of AIDS. Statistics in Medicine, 1989, 8: 103120.
17. Arca M, Perucci CA, Spadea T. The epidemic dynamics of HIV-1 in Italy: modelling the interaction between intravenous drug users and heterosexual population. Statistics in Medicine, 1992, 11: 16571684.
18. Kault DA. The impact of sexual mixing patterns on the spread of AIDS. Mathematical Biosciences, 1995, 128: 211241.
19. Brookmeyer R, Gail MH. Minimum size of the acquired immunodeficiency syndrome (AIDS) epidemic in the United States. Lancet, 1986, 2 (8519): 13201322.
20. Gail MH, Brookmeyer R. Methods for projecting course of acquired immunodeficiency syndrome epidemic. Journal of the National Cancer Institute, 1988, 80 (12): 900911.
21. Brookmeyer R, Damiano A. Statistical methods for short-term projections of AIDS incidence. Statistics in Medicine, 1989, 8: 2334.
22. Brookmeyer R, Liao J. Statistical modelling of the AIDS epidemic for forecasting health care needs. Biometrics, 1990, 46: 11511163.
23. Brookmeyer R. Reconstruction and future trends of the AIDS epidemic in the United States. Science, 1991, 253: 3742.
24. Rosenberg PS, Gail MH, Carroll RJ. Estimating HIV prevalence and projecting AIDS incidence in the United States: a model that accounts for therapy and changes in the surveillance definition of AIDS. Statistics in Medicine, 1992, 11: 16331655.
25. Rosenberg PS. Backcalculation models of age-specific HIV incidence rates. Statistics in Medicine, 1994, 13: 19751990.
26. Marion SA, Schecter MT. Use of backcalculation for estimation of the probability of progression from HIV infection to AIDS. Statistics in Medicine, 1993, 12: 617631.
27. Seydel J et al. Backcalculation of the number infected with human immunodeficiency virus in Germany. Journal of Acquired Immune Deficiency Syndromes, 1994, 7 (1): 7478.
28. Kaplan EH, Slater PE, Soskolne V. How many HIV infections are there in Israel? Reconstructing HIV incidence from AIDS case reporting. Public Health Reviews, 1995, 23: 215235.
29. Rosenberg PS, Gail MH, Pee D. Mean square error of estimates of HIV prevalence and short-term AIDS projections derived by backcalculation. Statistics in Medicine, 1991, 10: 11671180.
30. Solomon PJ, Wilson SR. Accomodating change due to treatment in the method of back projection for estimating HIV infection incidence. Biometrics, 1990, 46: 11651170.
31. Chin J, Lwanga SW. Estimation and projection of adult AIDS cases: a simple epidemiological model. Bulletin of the World Health Organization, 1991, 69: 399406.
32. Chin J, Lwanga S, Mann JM. The global epidemiology and projected short-term demographic impact of AIDS. Population Bulletin of the United Nations, 1989, 27: 5468.
33. Chin J. Global estimates of AIDS cases and HIV infections: 1990. AIDS, 1990, 4 (Suppl. 1): S277S283.
34. Mertens TE, Low-Beer D. HIV and AIDS: where is the epidemic going? Bulletin of the World Health Organization, 1996, 74: 121129.
35. Report on the global HIV/AIDS epidemic. Geneva, UNAIDS, June 1998 (document no. UNAIDS/98.10;WHO/EMC/ VIR/98.2; WHO/ASD/98.2).
36. Burton AH, Mertens TE. Provisional country estimates of prevalent adult human immunodeficiency virus infections as of end 1994: a description of the methods. International Journal of Epidemiology, 1998, 27: 101107.
37. Schwartlander B et al. Country-specific estimates and models of HIV and AIDS: methods and limitations. AIDS, 1999, 13 (17): 24452458.
38. Recent HIV seroprevalence levels by country: February 1999. Washington, DC, United States Bureau of the Census, 1999 (Research Note No. 26).
39. Epidemiological fact sheets on HIV/AIDS and sexually transmitted diseases. Geneva, World Health Organization, 1998 (document no. UNAIDS/98.13, WHO/EMC/VIR/98.3, WHO/ASD98.3).
40. Kengeya-Kayondo JF et al. Incidence of HIV-1 infection in adults and socio-demographic characteristics of seroconverters in a rural population in Uganda: 19901994. International Journal of Epidemiology, 1996, 25 (5): 10771082.
41. Leroy V et al. Four years of natural history of HIV-1 infection in African women: a prospective cohort study in Kigali (Rwanda), 19881993. Journal of Acquired Immune Deficiency Syndromes and Human Retrovirology, 1995, 9 (4): 415421.
42. Morgan D et al. An HIV-1 natural history cohort and survival times in rural Uganda. AIDS, 1997, 11 (5): 633640.
43. Nunn AJ et al. Mortality associated with HIV-1 infection over five years in a rural Ugandan population: cohort study. British Medical Journal, 1997, 315: 767771.
44. Okongo M et al. Causes of death in a rural, population-based human immunodeficiency virus type 1 (HIV-1) natural history cohort in Uganda. International Journal of Epidemiology, 1998, 27: 698702.
45. Borgdorff M et al. Sentinel surveillance for HIV-1 infection: how representative are blood donors, outpatients with fever, anaemia, or sexually transmitted disease, and antenatal clinic attenders in Mwanza Region, Tanzania. AIDS, 1993, 7 (4): 567572.
46. Berkley S et al. AIDS and infection in Uganda are more women infected than men? AIDS, 1990, 4 (12): 12371242.
1 Health Policy Analyst, Global Programme on Evidence for Health Policy, World Health Organization, 1211 Geneva 27, Switzerland (email: salomonj@who.int). Correspondence should be addressed to this author.
2 Executive Director, Evidence and Information for Policy, World Health Organization, Geneva, Switzerland.
a Use of aweighted average of the peak level and the unmodified gamma level was adapted from proposals by Dr Griffith Feeney and Dr Tim Brown following discussions at the meeting of the Reference Group on HIV/AIDS Estimates, Modelling and Projections (Geneva, Switzerland, 1011 June 1999).
Ref. No. 99-0139
