ARTIGO/ARTICLE
Malaria vaccines: lessons from field trials
Vacinas anti-maláricas: lições aprendidas em ensaios de campo
Claudio J. StruchinerI,II; M. Elizabeth HalloranIII,IV; Robert C. BrunetV; José M. C. RibeiroVI; Eduardo MassadVII
IDr. C. J. Struchiner was partially supported by the Brazilian Research Council (CNPq)
IIEscola Nacional de Saúde Pública, Fundação Oswaldo Cruz. Rua Leopoldo Bulhões, 1480, Rio de Janeiro, RJ, 21041-210, Brazil
IIIM. E. Halloran was partially supported by NIH NIAID FIRST Award R29-AI31057-04
IVDepartment of Biostatistics. Emory University School of Public Health 1518 Clifton Road NE, Atlanta, Georgia 30322
VDépartement de Mathématiques, Université de Montréal, C.P. 6128 Succursale A, Montréal, Quebec, CANADA H3C 3J7
VIDepartment of Entomology, The University of Arizona, Tucson, Arizona 85721
VIIFaculdade de Medicina da Universidade de São Paulo. Av. Dr. Arnaldo, 455, São Paulo, SP, 01246-904, Brazil
ABSTRACT
Malaria vaccine candidates have already been tested and new trials are being carried out. We present a brief description of specific issues of validity that are relevant when assessing vaccine efficacy in the field and illustrate how the application of these principles might improve our interpretation of the data being gathered in actual malaria vaccine field trials. Our discussion assumes that vaccine evaluation shares the same general principles of validity with epidemiologic causal inference, i.e., the process of drawing inferences from epidemiologic data aiming at the identification of causes of diseases. Judicious exercise of these principles indicates that, for meaningful interpretation, measures of vaccine efficacy require definitions based upon arguments conditional on the amount of exposure to infection, and specification of the initial and final states in which one believes the effect of interest takes place.
Key words: Malaria; Vaccine; Vaccine Efficacy; Field Trial
RESUMO
Vacinas candidatas contra a malária já foram testadas, e novos ensaios estão sendo realizados. Os autores apresentam uma breve descrição das questões específicas de validade que são relevantes para uma avaliação da eficácia de vacinas em campo e mostram como a aplicação desses princípios poderiam melhorar a interpretação dos dados coletados atualmente pelos ensaios de campo de vacinas anti-maláricas. A discussão pressupõe que a avaliação de vacinas compartilha os mesmos princípios gerais de validade com a inferência causal epidemiológica, i.é., o processo de fazer inferências a partir dos dados epidemiológicos, objetivando identificar as causas das doenças. A aplicação criteriosa desses princípios indica que, para haver uma interpretação significativa, as medidas de eficácia vacinal requerem definições baseadas em argumentos condicionais à quantidade de exposição à infecção e a especificação dos estados inicial e final onde acredita-se que ocorre o evento de interesse para o ensaio.
Palavras-Chave: Malária; Vacina; Eficácia da Vacina; Ensaio de Campo
INTRODUCTION
Malaria vaccine candidates have already been tested in the field (Valero et al., 1993; Noya et al., 1994; Sempértegui et al., 1994) and new trials are being carried out, most notably in Tanzania (Alonso et al., 1994; Teuscher et al., 1994), Thailand (WHO, 1993) and The Gambia (Travis, 1993). Both experimental and observational studies are potentially subject to biases which affect inferences based on them. The degree to which the studies meet basic logical criteria for absence of bias is known as validity in the epidemiological literature (Miettinen, 1985; Rothman, 1986). Being an epidemiologic study, vaccine field trials must satisfy general principles of validity applicable to the process of drawing inferences from epidemiologic data. The complex role played by the immune mechanisms in malaria, their implications for protection at the population level (herd immunity), and a disease transmission cycle mediated by vectors are important factors potentially contributing to lack of validity when evaluating the epidemiologic impact of malaria health interventions, in particular vaccines.
The interplay of these various aspects implies that incidence depends on the prevalence of the phenomenon under study, a condition known as dependent happenings (Ross, 1916). The design of valid studies under the conditions of dependent happenings and the definition of measures of vaccine efficacy discriminating between direct and indirect effects (Struchiner et al., 1990; Halloran & Struchiner, 1991) are needed when describing the impact of vaccines on individual time-dependent risk factors, infective history and the dynamic population process (Singer, 1984; Struchiner et al., 1990). General principles of validity in epidemiologic studies are discussed in more detail elsewhere (Miettinen, 1985; Rothman, 1986) under various classification schemes and terminology, the most commonly accepted being confounding, selection bias, and information bias. Problems stemming from the application of these principles under the specific conditions of dependent happenings have been receiving considerable attention more recently (Brunet et al., 1993; Comstock, 1994; Halloran et al., 1989; Halloran & Struchiner, 1991; Halloran et al., 1991; Halloran et al., 1992; Koopman et al., 1991; Struchiner et al., 1989; Struchiner et al., n/d; Susser 1994; Halloran & Struchiner, n/d). In the following sections we present a brief description of specific issues of validity that are relevant when assessing vaccine efficacy in the field. Further, we comment on how the application of these principles might improve our interpretation of the data being gathered in actual malaria vaccine field trials.
GENERAL PRINCIPLES OF VALIDITY IN VACCINE EVALUATION
Our discussion assumes that vaccine evaluation shares the same general principles of validity with epidemiologic inference. In particular, we are interested in drawing a parallel between what are accepted as good practices or guidelines for designing field trials to assess the efficacy of a vaccine, and the process of drawing inferences from epidemiologic data aiming at the identification of causes of diseases. These inferences are often made from non-experimental evidence. Halloran & Struchiner (n/d) provide the theoretical basis for the analogy between causal inference (Greenland & Robins, 1986; Holland, 1986; Rubin, 1978) and the assessment of efficacy of intervention programs under dependent happenings.
Figure 1 provides a convenient framework for organizing the discussion of general principles of validity in vaccine evaluation. It merges a very simple description of the sequence of pathogenic processes leading to the endpoint of interest that a vaccine is supposed to prevent (represented by boxes and arrows in continuous lines), and the relevant issues on the use of statistical models and selection of parameters (Gail, 1991) descriptive of the various concepts of vaccine efficacy (represented by boxes and arrows in dashed lines).
In this schematic representation of various aspects of design and analysis of vaccine field trials, the first dashed rectangle (A) represents vaccine status (V) and covariate levels (X) of each individual in the trial population. Vaccine status and covariate levels can both be either constant or time-dependent. Vaccine allocation and the role of randomization are important design considerations at this point.
Moving to the right in the diagram, we have the dashed rectangle (B) labeled "Exposure to Infection (E)". In field trials, vaccinated and unvaccinated individuals are exposed to infection, i.e. bitten by infected mosquitos, by natural means. Thus in practice, status E is not known or difficult to assess.
Rates le and lve describe the instantaneous probability of being bitten and are functions of time and other environmental and entomological factors. Good study design practices recommend that both rates be equal and lack of compliance with this recommendation is known as exposure bias (Halloran et al., 1994a).
Once exposed to infection, vaccinated and unvaccinated individuals might progress up to the endpoint of interest at rates lv and l0, respectively (dashed rectangle C). Both rates are dependent on time and covariates X. The main point of the trial is then to infer on the causal response model f(endpoint of interes | V, X, E). This task is usually very difficult because one does not have data on rates lv and l0, directly, but instead on total or compound rates lvt and lt which depict the transition from the susceptible vaccinated and unvaccinated states to the endpoint of interest. Valid studies should be able to reconstitute the desirable comparison lv to l0 from the observable comparison lvt to lt, which is hampered by missing latent structures (lack of knowledge on lve and le) or mis-modeling of available measurements (selection of wrong functional form f(.)).
Estimation of f(.) and especially the efficacy of the vaccine given exposure to infection is done in the analysis. Critical points at this step are the discrimination of epidemiologic categories of relevance among which the vaccine might behave heterogeneously, and discrimination of the epidemiologic mechanisms of action of the vaccine which will determine the choice of measure of disease frequency.
Different study designs are appropriate for vaccine evaluation. They all need to guarantee proper comparison of lv to l0 by carefully handling the various steps discriminated above. Other sources of systematic errors which will not be covered in this paper, such as the structure of missing data and errors in measurement of variables, can also bias estimates of vaccine efficacy. We expand on the topics mentioned above in what follows.
Comparison of Vaccinated and Unvaccinated
Exchangeability
In any epidemiologic study conceived to assess the effect of a certain treatment on an outcome of interest, comparison groups must be, in all material respects, alike except for their treatment status. The statement can be interpreted as if the same results would be expected if treatment status had been exchanged between the two groups. In other words, exchangeability assures comparability between treatment groups and is an important requirement for valid epidemiologic inference on the effects or causal role of the treatment of interest. Conversely, inherent differences in risk between treated and untreated individuals implies lack of comparability between treatment groups which could potentially bias the estimation of the effects of said treatment on disease risk, a condition known as confounding in epidemiology.
When the outcomes under study are independent (independent happenings), exchangeability guarantees that it would be possible to describe the occurrence of the outcome of interest among the treated individuals, had they not been treated, from the observed data on the untreated. The latter sentence describes only partially the concept of exchangeability but is sufficient to assure identifiability of causative parameters (Greenland & Robins, 1986) in chronic disease epidemiology, where happenings are independent. Complete exchangeability must also guarantee that it would be possible to describe the occurrence of the outcome of interest among the untreated individuals, had they been under treatment, from the observed data on the treatment group.
The requirement that the vaccinated and unvaccinated be exchangeable was noted as early as 1915 by Greenwood and Yule in their criteria for valid efficacy or effectiveness studies. Field trials that comply with this requirement are believed to yield unconfounded estimates of vaccine efficacy. This belief stems from the analogy one could make between a vaccine and the treatment factor in epidemiologic studies. However, direct application to vaccine field trials of the concepts briefly described in the previous two paragraphs is not possible without further qualification. Returning to Figure 1, we notice that comparison of rates lt and lvt requires that the epidemiologic compartments (susceptible unvaccinated and susceptible vaccinated) in dashed rectangle A be exchangeable. Yet, comparison of rates l0 and lv require exchangeability between vaccinated and unvaccinated individuals that were actually exposed to infection as depicted in dashed rectangle C of Figure 1. Halloran & Struchiner (n/d) separate evaluation of vaccines on the one hand, conditional on exposure to infection, and on the other hand, not conditioning on exposure to infection.
Thus, we must be aware that the concept of vaccine efficay is not unique and be explicit about our intents. In addition, since exchangeability within both pairs of comparison groups does not necessarily hold simultaneously, field trials that yield valid measures of vaccine efficacy of one kind can potentially lead to biased estimates of efficacy of a different kind.
By the same token, partial and complete exchangeability must also be further qualified. Partial exchangeability is expressed as the counterfactual reasoning requiring that the ideal unvaccinated control group describe the potential outcome in the vaccinated group in the absence of vaccination. In actual field trials, however, due to the indirect protection of the unvaccinated group which is brought about by the presence of the individuals who became immune by the vaccine, a mechanism known as herd immunity (Fine, 1993), even partial exchangeability might not be achieved giving rise to different concepts of vaccine efficacy (Halloran & Struchiner, 1991; Halloran et al., 1991). Complete exchangeability requires, in addition, that the outcome observed in the vaccinated subjects describe the potential outcome in the unvaccinated group had it been vaccinated, or, phrasing it in a different way, if vaccination states were exchanged, the value observed for the incidence among vaccinated and unvaccinated subjects would have been the same. Again, due to the indirect effects of a vaccine, the latter statement gives rise to different interpretations. This translates into different concepts of measures of vaccine efficacy that are discussed below.
The principle of exchangeability in actual vaccine field trials thus involves at least two dimensions: (i) where in the sequence of pathogenic processes comparisons between vaccinated and unvaccinated is being sought, as exemplified by the epidemiologic compartments in dashed rectangles A and C in Figure 1; and (ii) how we interpret the counterfactual reasoning implicit in the principle of exchangeability. We will see next that dimension (i) leads to the concept of biological efficacy and dimension (ii) to the concepts of direct and indirect effects of a vaccine. It then becomes a challenge to epidemiologists to design studies where comparability is ensured and to statisticians to develop methods to control for departures from the exchangeability principle.
Randomization and Double-blinding
Actual study populations are often heterogeneous in biological, social or environmental characteristics relevant to the validity of vaccine field trials. These heterogeneities result in differences in susceptibility, exposure to infection, outcome assessment and propensity to loss to follow up. Sometimes a few of these factors can be identified and measured and are represented by the vector of covariates X in Figure 1. Such measured differences can be controlled for in the analysis. Most sources of heterogeneity, or lack of comparability among study subjects, however, remain unknown. Randomization and double-blinding are two strategies designed to distribute these unmeasured heterogeneities approximately equally between the comparison groups. These strategies, often contained in guidelines for designing vaccine trials (WHO, 1986), are not invalidated by the presence of heterogeneities.
It is thus worth reviewing (Greenland, 1990) some misconceptions about randomization and what is actually achieved by this treatment (vaccine) assignment mechanism. First of all, it is important to notice that randomization does not prevent confounding, the epidemiologic bias defined above in terms of lack of comparability or exchangeability. On the other hand, randomization prevents statistical bias since trials conducted this way yield estimates that do not deviate in average from the expected value of the probability distribution describing possible results of the trial. Even if the statistical concept of bias and the epidemiologic concept of confounding differ, randomization does have an effect on confounding. Often, it is possible to diminish the probability of important confounding by increasing the sizes of the treatment groups. Rubin (1991) reviews the critical role of random and nonrandom assignment mechanisms under four modes of statistical inference for causal effects.
Random assignment of vaccine treatment does not restore exchangeability and the statistical benefits of randomization do not necessarily propagate to further steps in the sequence of pathogenic processes. Thus, if study subjects are randomly assigned to the two epidemiologic compartments in the dashed rectangle A of Figure 1, as is usually the case, that does not necessarily imply that the same statistical benefits will be preserved when comparing rates l0 and lv between the epidemiologic compartments in dashed rectangle C of Figure 1. Similarly, random assignment of a vaccine is a static attribute which is not preserved over time. The statistical benefits of randomization can be lost as the comparison groups evolve in time. Baseline transmission rate, active and passive case accrual and treatment availability are likely to change as the trial progresses.
Complementing the requirement for valid comparisons of vaccinated and unvaccinated, Greenwood & Yule (1915: 115-116) also indicate that the "criteria of the fact of inoculation and of the fact of disease having occurred must be independent". Again, the vaccine allocation mechanism should preserve exchangeability in the sense defined above. Nonrandom allocation jeopardizes the principle of exchangeability. On the other hand, randomization does not necessarily guarantee exchangeability.
Equal Exposure to Infection
Greenwood & Yule (1915: 115-116) noticed, in addition, that validity of comparison of the groups also require that the "effective exposure to the disease must be identical in the case of the inoculated and uninoculated persons". While the necessity of comparability of personal attributes in the two groups is common to epidemiologic studies in chronic and infectious diseases, the requirement of comparability of exposure to infection is specific to epidemiologic studies in infectious diseases and more subtle to fulfill. Notice that exposure to infection might be the same within any trial (le = lve) but the study population participating in trials taking place at other locations and time may be subject to different baseline inoculation rates rendering comparison of measures of vaccine efficacy across geographic locations or time more difficult. Equal amount of exposure to infection in the vaccinated and unvaccinated groups is an important requirement for the assumption of exchangeability to hold. Valid comparisons, however, must be further qualified by making explicit reference to the underlying level of exposure to infection in order to be appropriately interpreted. It is well known that the background level of transmission is a function of seasonal factors (density of mosquitos, climate, etc.), other concomitant control measures besides the vaccine, and changes in transmission brought by the vaccine itself.
The importance of the baseline transmission levels for the definition of appropriate measures of vaccine efficacy can be exemplified as follows. Figure 1 depicts a schematic representation of a sequence of pathogenic steps simplified to just three states (full line). In this particular example we are considering three epidemiologic compartments and two transition rates of interest when evaluating vaccine efficacy. Susceptible individuals are exposed to infection according to rates le and lve, supposed equal in this example. Unvaccinated individuals exposed to infection progress to the endpoint of interest at the rate l0. In most instances, as is the case of sporozoite and merozoite vaccines, it is expected that a vaccine decreases l0 to lv, the transition rate between the latter two compartments among the vaccinated. Gametic vaccines are expected to change le but this instance is not being considered in the diagram. Vaccines that primarily affect l0 might also affect le indirectly through a mechanism known as herd immunity. It is very difficult in the field to estimate the transition rates for the individual steps and one has to settle for compound rates lt and lvt describing transition from the susceptible and the susceptible vaccinated states to the endpoint of interest, respectively. The mean duration of being in a given compartment is equal to the reciprocal of the rate at which individuals leave this compartment and thus, the compound rate can be calculated from the individual rates as follows:
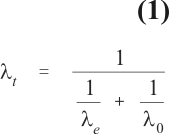
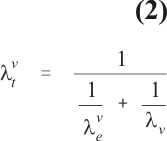
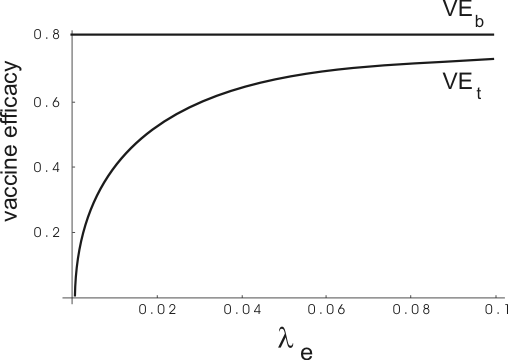
Vaccines that protect individuals from infection and morbidity affect primarily l0 and one could argue that measures of vaccine efficacy based on l0 and lv better estimate the biological effect of interest, and that the changes in leand lve are, regarding estimation of the direct effect of a vaccine, seen as noninformative and a nuisance factor, the exposure bias (Halloran et al., 1994a). Let VEb = 1 lv/l0 and VEt = 1 lvt/lt denote measures of vaccine efficacy based on both concepts. Suppose now that lv is a constant fraction of l0 and that le is constant and common to both groups describing vaccination status. Figure 2 shows that VEb differs from VEt and the difference decreases as le increases. The point made here could be generalized in two ways. First, the sequence of pathogenic effects could grow more complex by incorporating additional concepts from other fields such as immunology, molecular biology, parasitology, etc. leading to an increase in the number of compartments and more detailed transition dynamics. Second, changes occurring at specific points in the sequence might indirectly affect other points differently among vaccinated and unvaccinated individuals, rendering the functional dependence of compound rates on nuisance rates more difficult to understand. Hence, measures of vaccine efficacy based on compound rates do not bear a clear relationship to measures based on more specific biological concepts and tend to underestimate biological efficacy. Biological efficacy and types of effects of a vaccine are discussed in more details in the next sections.
FIGURE 2. VEb and VEt as a Function of le
Vaccines that are efficacious are expected to affect transmission of infection. In doing so, these vaccines could potentially modify exposure to infection among vaccinated and unvaccinated people as compared to transmission prior to vaccination. If the reduction is equal for both groups, then the two groups are still equally exposed. The outcomes are not exchangeable with what they would have been without the intervention (Halloran & Struchiner, n/d). On the other hand, the exposure to infection might be differentially reduced by the intervention, challenging, in this way, the requirement of equality of effective exposure to infection in both groups (Comstock, 1990). Seen from this perspective, valid studies for assessing vaccine efficacy would never become possible, a strange paradox, unless the problem could be avoided by the choice of clever study designs or controlled for by appropriate analytical tools. Notice that this behavior is not observed when one is dealing with zoonotic diseases in which the presence of an animal reservoir preserves the transmission level or when vaccine coverage is low.
We have raised potential sources of problems challenging the principle of exchangeability. In actual malaria vaccine trials, it is difficult to correlate observed changes in the frequency of the endpoint of interest to the effect of a vaccine because parasite load received by each participant in the trial, vaccinated or not, is not known to the investigator. It is possible to try to separate exposure to infection from susceptibility to infection formally, the latter being affected by a vaccine (Rhodes et al., 1994). Data on actual exposure to infection are scarce, but could indirectly be approximated by surrogate variables that are easier to collect. Variables that could help in controlling for differences in exposure to infection include time since arrival in the endemic area, reported number of previous malaria episodes, clinical signs (splenomegaly), and, possibly, serology at the start of follow up period. The same objective could be achieved by taking advantage of the observed clustering of cases within households in the same village. It seems that individuals living in the same household are more homogeneously exposed to infection, therefore, trials that compare vaccinated to unvaccinated persons matched on household are less prone to bias from differences in exposure to infection. Finally, one could reconstitute exchangeability by the appropriate use of mathematical models. Data collected prior to the intervention helps to project the baseline transmission level into the post intervention period, allowing for the construction of a comparison standard estimating what exposure to infection would have been in the absence of intervention.
In summary, in order to assure validity of comparison one must guarantee, through appropriate mechanisms of vaccine assignment, exchangeability according to the various aspects of the transmission process, ie., the infectivity of the infectious source, the susceptibility of the susceptible, and the type of contact of the susceptible with the infectious source.
Model Specification
Ideally, analytical models to evaluate vaccine efficacy ought to specify the biological modes of action of a vaccine, the types of effects one intends to detect, and how these effects translate into actual measures of disease frequency. The better the available knowledge about the underlying biological processes of the disease in question, the more complete can be the sequence of pathogenic processes and diverse can be the possible modes of action of vaccines included in the model. For example, vaccines might modify the chances of a vaccinated person to acquire infection (eg. sporozoite vaccine), modify the incubation period (eg. some AIDS vaccines), modify morbidity (eg. merozoite vaccine), or modify transmission to vectors or other susceptibles (eg. gametic vaccine).
Biological Efficacy
Discussion of the relative merits of each measure of vaccine efficacy must begin with the definition of the basic concept of biological efficacy. How and where in the sequence of pathogenic processes the biological effect of a vaccine takes place is specified by its mode of action. Let us denote the sequence of pathogenic processes by states S0 ® S1®... ® Sp ® Sp + 1® ... ® Sn and let the vaccine affect the sequence at Sp® Sp + 1. By pathogenic processes, one might also include processes describing transmission of infection to vectors. Let, in addition, Iv and I0 denote the transition rates from pathogenic state Sp to Sp + 1 in the vaccinated and unvaccinated groups, respectively. Hence, biological efficacy can be defined as 1 Ir where Ir = Iv/I0. Ir can also be interpreted as the change in the instantaneous probability of transition from state Sp® Sp + 1 caused by the vaccine. Recall that validity of comparison requires that vaccinated and unvaccinated groups be exchangeable in all senses described previously, in particular vaccinated and unvaccinated must be subjected to the same amount of exposure to infection. Molineaux (1991) suggests breaking down the various steps in the malaria process according to sequence: uninfected ® prepatent infection ® patent parasitemia ® mild disease ® severe disease ® death. Halloran et al. (1994b) present the terminology one minus the relative reduction in pathogenicity for the vaccine effect on reducing the probability or rate of developing disease once infection has taken place, and one minus the relative residual infectiousness as the measure of efficacy in reducing transmission to a susceptible.
Precise knowledge of the states Sp and Sp +1 where the vaccine is affecting the sequence of pathogenic effects might be unavailable either because it is impossible to measure them or because practical considerations dictate that data be collected on other states. The overall rate for multiple stages is less than the lowest component transition rate (Morrison, 1979). Thus, for any given biological protection, different measures of efficacy can be estimated depending on the baseline point of departure and the outcome picked by the investigator. The outcome measures could have different, possibly nonlinear relationships to the underlying biological efficacy.
Types of Effects
One must also distinguish between direct and indirect effects of a vaccine when constructing a model to evaluate efficacy. Calling upon the principle of exchangeability once more, we can think of at least two pairs of facts and their corresponding counterfacts of interest for evaluation. The comparison of an outcome in a vaccinated individual and what the outcome would have been without the vaccine, all other things remaining equal, defines the direct effect of this vaccine. On the other hand, the indirect effect of a vaccine on individuals compares the outcome in an unvaccinated person in a population covered by the vaccine and what the outcome would have been in this very same unvaccinated person in a similar population with no vaccine coverage. Indirect effects depend on the level of vaccine coverage in the population. In real situations both effects take place simultaneously. One must construct measures of vaccine efficacy that reflect either concept or a combination of them.
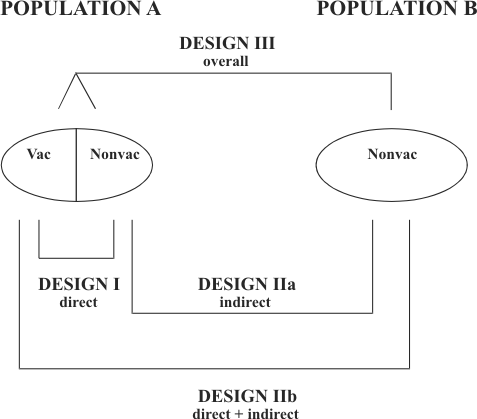
The search for the perfect unvaccinated control exchangeable with a vaccinated individual leads to non-unique answers as is exemplified in Figure 3. It is possible to define four study designs based on different pairs of comparison populations and the type of effect they are intended to evaluate (Struchiner et al., 1990; Halloran & Struchiner, 1991). One assumes a population A in which an intervention program takes place, and a population B, identical but separate from A in all aspects relevant to the transmission dynamics, in which no intervention takes place. Data on baseline transmission collected prior to the intervention could play the role of population B. In study design I, one intends to estimate direct effects. Vaccinated and unvaccinated are assumed to be subjected to the same exposure to infection since they are exposed to the same population of mosquitos, however, the actual level of exposure to infection might be known or not. In study design IIa, the nonvaccinated in population A is compared to the nonvaccinated in population B. This design estimates the indirect effects caused by changes in level of transmission due to vaccination. Study design IIb estimates both effects, direct and indirect, simultaneously. Design III takes the perspective of the population comparing overall rates in the vaccinated population A to unvaccinated population B. Each study design interprets in a different way the answer to the principle of exchangeability.
FIGURE 3. Study Designs for the Evaluation of the Different Effects of a Vaccine
Mis-modeling of Available Measurements
Lack of observance of the principle of exchangeability also happens when one fails to discriminate between the various epidemiologic categories of interest. Taking a very simplistic view, it is possible to represent (Dietz et al., 1974; Halloran et al., 1989; Halloran & Struchiner, 1992; Nedelman, 1984; Struchiner et al., 1989) several aspects of malaria transmission and immunity with a minimum set of compartments. These include nonparasitemic states discriminating two levels of immunity, non-immune (X1) and naturally immune (X3); and parasitemic states discriminating between immunes with mild symptoms (Y3) and non-immunes with serious disease (Y2), the latter compartment subdivided in turn into infectious (Y1) and non infectious individuals. In actual field trials, it might be difficult to identify categories X1 and X3, so vaccine is randomly assigned with both groups pooled together. Category X3 can be regarded as noninformative, or at least less informative, in this context due to their natural immunity. Thus, irrespective of the random assignment mechanism, lack of discrimination between groups X1 and X3 yield estimates of measures of vaccine efficacy which tend to underestimate the effect one would get by testing the vaccine only in individuals of type X1. The extent of this bias is proportional to the endemic level, since the higher the baseline level of transmission, the greater the contingent X3 and hence the greater the bias toward the null of measures that fail to discriminate the two categories.
Similarly, another mechanism leading to underestimation of the biological efficacy of a vaccine, irrespective of the random assignment mechanism is to include among the vaccinated contingent individuals in whom the vaccine has waned (Struchiner et al., 1990, Farrington, 1992). In the previous two examples, the direction of the bias could have been reversed had the vaccine conferred extra protection to naturally immune individuals. The discussion in this section reinforces the distinction between statistical bias and confounding, showing that randomized trials do not necessarily yield unconfounded estimates which can only be achieved when comparability validity between groups is attained.
Analysis
Choice of Measures of Disease Frequency
Epidemiologic data collected in the field is usually reported either as time to event or whether an event occurred in a specified time interval of observation. The first version allows us to calculate rates (incidence, hazard, force of infection). The second leads to the notion of risk (cumulative incidence, attack rate). Rate measures are more informative than risk measures in the sense that it is possible to reconstitute risks from rates, the opposite not being true except if assumptions, non-verifiable with the data, are made. Measures of vaccine efficacy can be constructed based on either concept. Rhodes et al. (1994) consider the different parameters of vaccine efficacy as a hierarchy depending on how much information is available on exposure to infection and time of events.
A simple example illustrates the relationship between measures of disease frequency, measures of efficacy and modes of action of a vaccine. Suppose that the number of susceptibles, N(t), decreases exponentially when subjected to a constant infection rate, l according to the expression N(t) = N0e-lt, where N0 is the number of susceptibles at the beginning of follow-up (Figure 4). Depletion of susceptibles can also be described based on a risk concept, i.e., the probability of becoming infected within a given time interval, t. The latter concept is known as attack rate, AR(t), a misnomer since it is not a rate. AR(t) can be expressed as a function of l,
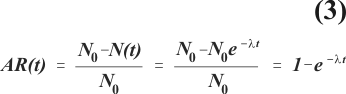
where N0 is the population of susceptibles at the beginning of follow-up, and N(t) denotes the remaining population of susceptibles after time interval t. Suppose that among vaccinated individuals the infection rate, lv, is a constant fraction of the infection rate among unvaccinated individuals, l0. Vaccine efficacy based on the ratio of these two rates is then constant and depicted by the horizontal straight line in figure 5. However, vaccine efficacy based on the ratio of attack rates, VEAR (t),
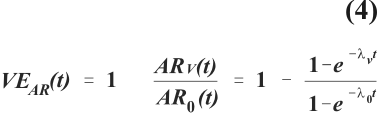
decreases as l0 increases showing that the same biological effect of a vaccine leads to divergent measures of vaccine efficacy depending on the choice of measure of frequency of the endpoint of interest.
FIGURE 4. Number of Susceptibles (N(t)) as a Function of Time

FIGURE 5. Divergent Measures of Vaccine Efficacy Depending on the Choice of Measure of Frequency of the Endpoint of Interest

Sources of Heterogeneity
Measures of vaccine efficacy in the field do not necessarily estimate biological efficacy and various factors concur for possible discrepancies. Individuals are heterogeneous regarding their susceptibility to infection, development and duration of natural immunity, etc. They also react differently once vaccinated, and immune responses ranging from total lack of protection to protection that is partial or complete are found for the different vaccines. Other sources of heterogeneity include vector behavior or competency, seasonal variations in climate, spatial clustering, and age-related inoculation rates or immunity.
We saw previously that the longer the period of observation and the higher the incidence of disease the greater the discrepancy between measures based on risk and measures based on incidence. The interpretation of measures of efficacy constructed from both notions is further complicated by heterogeneities from all sources mentioned. Under heterogeneity one has the choice to report stratum-specific or summary measures of effect, the latter representing weighted means of stratum specific measures. It is well known that both measures might differ depending on the distribution pattern of vaccine coverage among the various strata (Halloran et al., 1992).
EXAMPLES
In this section we illustrate some of the concepts discussed above by drawing examples from actual malaria vaccine field trials. These studies differ in various aspects and we have selected just a few of them. Our intent here is not to criticize the cited studies, but merely to use them to highlight difficulties in the interpretation of estimates of measures of vaccine efficacy in the field.
Randomized Study and Cumulative Risk Based Measure of Vaccine Efficacy
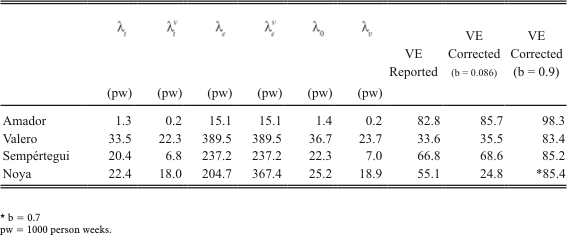
Amador et al. (1992) report on the results of the first field trials performed to assess the protectivity of the chemically synthesized malaria vaccine SPf66. They conducted a randomized trial in volunteers of the Colombian Military forces and used a measure of vaccine efficacy based on cumulative risk which compares probabilities of getting the disease at the end of follow-up between vaccinated and unvaccinated groups. Risk or probability of becoming diseased by P. falciparum in the placebo group was 4.76%, or 4 cases in a population of 84. Assuming a constant incidence rate and a 39 week follow up period, we can calculate the baseline incidence rate (lt) by expression (3) which yields an estimate of 1.3 cases per 1000 person-week (pw). Similarly, the transmission rate in the vaccinated group (lvt) is 0.2 pw.
Using a very crude approximation, we can estimate le from their data. Notice that le expresses the number of bites in humans by sporozoite positive mosquitos per unit of person time, a concept known in the malaria literature as the entomological inoculation rate. The incidence rate lt, or effective inoculation rate in the malaria literature, is calculated as the proportion b of the entomological inoculation rate resulting in the development of a brood of parasites. Nedelman (1984) estimated b as 0.086 from the Garki Project. We can estimate le from the expression lt = ble. Since the trial described by Amador et al. is randomized, we can assume as a first approximation that le = ble.
Carrying out these approximate calculations, it is possible to estimate l0 and lv by using expressions (1) and (2), respectively. The corrected value of vaccine efficacy follows from the relation VE = 1 - (lv / l0). Table 1 summarizes the various parameter estimates and presents the corrected estimates of vaccine efficacy for b = 0.086 and b = 0.9. The arbitrary choice of b was made to illustrate the sensitivity of the efficacy estimates to this parameter. The lower value of b which was calculated for a situation of higher endemicity also reflects a higher level of natural immunity. A higher level of b is more appropriate to describe nonimmune populations.
TABLE 1. Corrected Measures of Vaccine Efficacy for Different Entomological Inoculation Rates
Randomized Study and Incidence Rate Based Measure of Vaccine Efficacy
Valero et al. (1993) and Sempértegui et al. (1994) both report on the results of randomized double-blind placebo-controlled malaria vaccine field trials in Colombia and Ecuador, respectively. Rates lt and lt were directly estimated from the data, and rates le, lve, l0 and lv as well as VE can be calculated as above for b = 0.086 and b = 0.9. The results are summarized in Table 1.
Non-randomized Study and Incidence Rate
Based Measure of Vaccine Efficacy
Noya et al. (1994) reports on a non-randomized population-based clinical trial with the SPf66 synthetic P. falciparum malaria vaccine conducted in Venezuela. In this instance, one cannot assume le = lve and the authors suggest estimating the protective efficacy conferred by the vaccine by taking the ratio of the incidence rate during the follow-up period to the baseline incidence rate for the same calendar period prior to vaccination as a way to control for seasonal variation in incidence. Let lp and lvp denote, analogously to lt and lt ,the compound rate of transition from the susceptible state to the outcome of interest. Following the author's suggestions, rates le and le can be calculated from the relations lp = ble and lvp = blvefor b = 0.086 and b = 0.7. Remaining rates are calculated as indicated in subsection 3.1. A value of b=0.9 would yield a negative value for l0. The results are presented in Table 1.
This simple exercise shows that measures of vaccine efficacy based on compound rates underestimates measures of efficacy conditional on exposure. The difference between the two measures is a function of the entomological inoculation rate. Therefore, considerable efforts should be made to collect data to estimate le and lve.
DISCUSSION
In summary, it is expected that single or compound biological effects of any malaria vaccine will manifest through a variety of outcomes. The purpose of malaria vaccine trials is, therefore, to estimate the biological effect(s) of a vaccine and its (their) multiple outcomes. The latter can be classified as direct, indirect, total and overall effects according to the choice of a standard of comparison, ie., according to the counterfactual arguments and the level of observation, individual vs. population. Judicious exercise of the exchangeability principle can help in discriminating among the various outcomes. These are often time- and space-dependent phenomena that make single epidemiologic efficacy measures difficult to interpret biologically. For meaningful interpretation, measures of efficacy require specification, among other things, of the initial and final states one believes the effect of interest takes place, and of the amount of exposure to infection. Operational definitions of change in status defined by longer steps in the sequence of pathogenic processes, which include the change of status of interest but are not restricted to it, and efficacy measures which lack conditioning on exposure to infection underestimate their counterparts, i.e., measures based on precise definition of change in status and conditioned on exposure to infection. One should also guard against possible information and selection biases by choosing vaccine allocation mechanisms which are independent of case accrual.
REFERENCES
ALONSO, P. L.; TANNER, M.; SMITH, T.; HAYES, R. J.; AMRSTRONG SCHELLENBERG, J.; LOPEZ, M. M.; BASTOS DE AZEVEDO, I.; MENENDEZ, C.; LYIMO, E.; WEISS, N.; KILAMA, W. L. & TEUSCHER, T., 1994. A trial of the synthetic malaria vaccine SPf66 in Tanzania: Rationale and design. Vaccine, 12: 181-186.
AMADOR, R.; MORENO, A.; VALERO, V.; MURILLO, L.; MORA, A. L.; ROJAS, M.; ROCHA, C.; SALCEDO, M.; GUZMAN, F.; ESPEJO, F.; NUNEZ, F. & PATARROYO, M. E., 1992. The first field trials of the chemically synthesized malaria vaccine SPf66: Safety, immuno-genicity and protectivity. Vaccine, 10: 179-184.
BRUNET, R. C.; STRUCHINER, C. J. & HALLORAN, M. E., 1993. On the distribution of vaccine protection under heterogeneous response. Mathematical Biosciences, 116: 111-125.
COMSTOCK, G. W., 1994. Evaluating vaccination effectiveness and vaccine efficacy by means of case-control studies. Epidemiologic Reviews, 16: 77-89.
_____, 1990. Vaccine evaluation by case-control or prospective studies. American Journal of Epidemiology, 131: 205-207.
DIETZ, K.; MOLINEAUX, L. & THOMAS, A., 1974. A malaria model tested in the African savannah. Bulletin of the World Health Organization, 50: 347-357.
FARRINGTON, C. P., 1992. The measurement and interpretation of age-specific vaccine efficacy. International Journal of Epidemiology, 21: 1014-1020.
FINE, P. E., 1993. Herd immunity: History, theory, practice. Epidemiologic Reviews, 15: 265-302.
GAIL, M. H., 1991. A bibliography and comments on the use of statistical models in epidemiology in the 1980s. Statistics in Medicine, 10: 1819-1885.
GREENLAND, S., 1990. Randomization, statistics, and causal inference. Epidemiology, 1: 421-429.
GREENLAND, S. & ROBINS, J. M., 1986. Identifiability, exchangeability, and epidemiologic confounding. International Journal of Epidemiology, 15: 412-418.
GREENWOOD, M. & YULE, U. G., 1915. The statistics of anti-typhoid anti-cholera inoculations, and the interpretation of such statistics in general. Proceedins of the Royal Society of Medicine, 8 (part 2): 113-194.
HALLORAN, M. E. & STRUCHINER, C. J., 1991. Study designs for dependent happenings. Epidemiology, 2: 331-338.
_____, 1992. Modeling transmission dynamics of stage-specific malaria vaccines. Parasitology Today, 8: 77-85.
_____, (n/d). Causal inference for dependent happenings. Epidemiology. (to appear)
HALLORAN, M. E.; HABER, M. & LONGINI Jr., I. M., 1992. Interpretation and estimation of vaccine efficacy under heterogeneity. American Journal of Epidemiology, 136: 328-343.
HALLORAN, M. E.; HABER, M. & LONGINI Jr., I. M. & STRUCHINER, C. J., 1991. Direct and indirect effects in vaccine efficacy and effectivenes. American Journal of Epidemiology, 133: 323-331.
HALLORAN, M. E.; LONGINI Jr., I. M.; HABER, M. & STRUCHINER, C. J., 1994a. Exposure efficacy and change in contact rates in evaluating prophylatic HIV vaccines in the field. Statistics in Medicine, 13: 357-377.
HALLORAN, M. E.; STRUCHINER, C. J. & SPIELMAN, A., 1989. Modelling malaria vaccines II: Population effects of stage-specific malaria vaccines dependent on natural boosting. Mathematical Biosciences, 94: 115-149.
HALLORAN, M. E.; STRUCHINER, C. J. & WATELET, L., 1994b. Epidemiologic effects of vaccines with complex direct effects in an Age-structured population. Mathematical Biosciences, 121: 193-225.
HOLLAND, P. W., 1986. Statistics and causal inference (with discussion). Journal of the American Statistical Association, 81: 945-960.
KOOPMAN, J. S.; LONGINI Jr., I. M.; JACQUEZ, J. A.; SIMON, C. P.; OSTROWM, D. G.; MARTIN, W. R. & WOODCOCK, D. M., 1991. Assessing risk factors for transmission of infection. American Journal of Epidemiology, 133: 1199-1209.
MIETTINEN, O. S., 1985. Theoretical Epidemiology. Principles of Occurrence Research in Medicine. New York: John Wiley & Sons.
MOLINEAUX, L., 1991. Waiting for the Vaccine. London School of Hygiene and Tropical Medicine First Annual Public Health Forum. Workshop Report and Recommendations. New York: John Wiley & Sons.
MORRISON, A. S., 1979. Sequential pathogenic components of rates. American Journal of Epidemiology, 109: 709-718.
NEDELMAN, J., 1984. Inoculation rate and recovery rates in the malaria model of Dietz, Molineaux, and Thomas. Mathematical Biosciences, 69: 209-233.
NOYA, O.; BERTI, Y. G.; NOYA, B. A.; BORGES, R.; ZERPA, N.; URBÁEZ, J. D.; MADONNA, A.; GARRIDO, E.; URBÁEZ, M.; BORGES, R. E.; GARCIA, P.; REYES, I.; PRIETO, W.; COLMENARES, C.; PABÓN, R.; BARRAEZ, T.; DE CACERES, L. G.; GODOY, N. & SIFONTES, R., 1994. A population-based clinical trial with the SPf66 synthetic P. falciparum malaria vaccine in Venezuela. The Journal of Infectious Diseases, 170: 396-402.
RHODES, P. H.; HALLORAN, M. E. & LONGINI Jr., I. M., 1994. Counting process models for differentiating exposure to infection and susceptibility. Atlanta: Division of Biostatistics, Emory University School of Public Health. (Technical Report, 1) (Mimeo.)
ROSS, R., 1916. An application of the theory of probabilities to the study of a priori pathometry, i. Proceedings of the Royal Society of Medicine Series A, 92: 204-230.
ROTHMAN, K. J., 1986. Modern Epidemiology. Boston: Little Brown.
RUBIN, D. B., 1978. Bayesian inference for causal effects: The role of randomization. Annals of Statistics, 7: 34-58.
_____, 1991. Practical implications of modes of statistical inference for causal effects and the critical role of the assignement mechanism. Biometrics, 47: 1213-1234.
SEMPÉRTEGUI, B.; ESTRELLA, B.; MOSCOSO, J.; PIEDRAHITA, L.; HERNÁNDEZ, D.; GAYBOR, J.; NARANJO, P.; MANCERO, O.; ARIAS, S.; BERNAL, R.; CÓRDOVA, M. E.; SUÁREZ, J. & ZICKER, F., 1994. Safety, immuno-genicity and protective effect of the SPf66 malaria synthetic vaccine against Plasmodium falciparum infection in a randomized double-blind placebo-controlled field trial in an endemic area of Ecuador. Vaccine, 12: 337-341.
SINGER, B., 1984. Mathematical models of infectious diseases: Seeking new tools for planning and evaluating control programs. Population and Development Review, (suppl.): 347-365. (Child Survival)
STRUCHINER, C. J.; BRUNET, R. C.; HALLORAN, M. E.; MASSAD, E. & AZEVEDO-NETO, R., (n/d). On the Use of State-Space Models for the Evaluation Health Interventions. Winnipeg: Wuerz Publishing Ltd. (to appear)
STRUCHINER, C. J.; HALLORAN, M. E., ROBINS, J. M. & SPIELMAN, A., 1990. The behaviour of common measures of association used to assess a vaccination programme under complex disease transmission patterns: a computer simulation study of malaria vaccines. International Journal of Epidemiology, 19: 187-196.
STRUCHINER, C. J.; HALLORAN, M. E. & SPIELMAN, A., 1989. Modelling malaria vaccines I: New uses for old ideas. Mathematical Bio-sciences, 94: 87-113.
SUSSER, M., 1994. The logic in ecological: I. the logic of analysis. American Journal of Public Health, 84: 825-829.
TEUSCHER, T.; ARMSTRONG SCHELLENBERG, J. R. M.; BASTOS DE AZEVEDO, I.; HURT, N.; SMITH, T.; HAYES, R.; MASANJA, H.; SILVA, Y.; LOPEZ, M. C.; KITUA, A.; KILAMA, W.; TANNER, M. & ALONSO, P. L., 1994. SPf66, a chemically synthesized subunit malaria vaccine, is safe and immunogenic in Tanzanians exposed to intense malaria transmission. Vaccine, 124: 328-336.
TRAVIS, J., 1993. U.K. changes mind about malaria vaccine. Science, 261: 1392.
VALERO, M. V.; AMADOR, L. R.; GALINDO, C.; FIGUEROA, J.; BELLO, M. S.; MURILLO, L. A.; MORA, A. L.; PATARROYO, G.; ROCHA, C. L.; ROJAS, M.; APONTE, J. J.; SARMIENTO, L. E.; LOZADA, D. M.; CORONELL, C. G.; ORTEGA, N. M.; ROSAS, J. E.; ALONSO, P. L. & PATRROYO, M. E., 1993. Vaccination with SPf66, a chemically synthesised vaccine, against Plasmodium falciparum malaria in Colombia. The Lancet, 341: 705-710.
WHO (World Health Organization), 1986. Guidelines for the epidemiological evaluation of Plasmodium falciparum sporozoite vaccines. TDR/MAP/SVE/PF/86.5. Geneva: WHO. (Mimeo.)
_____, 1993. Vaccine protection. Working paper prepared for the WHO/PAHO/Instituto de Inmunologia consultation on Future Implementation of Malaria Vaccines, Santafé de Bogotá, Colombia, 3-4 September. (Mimeo.)
