Abstract:
Obesity is considered a serious public health problem, as an epidemic disease with major global repercussions that is associated with the development of other chronic conditions such as hypertension, diabetes, and cardiovascular diseases. The current study examines the distribution of adult obesity in different countries using a beta regression model. This is a descriptive ecological study with a quantitative and inferential approach and a focus on beta regression analysis. Application of this method used a set of real data from public sources on adult obesity in 78 countries in 2014. Descriptive data analysis showed that 50% of the countries showed adult obesity prevalence greater than 20%. In addition, analysis of the distribution of prevalence by country showed lower adult obesity levels in countries of Asia and Africa. Meanwhile, higher values were found in countries of the Americas and Europe. Boxplot analysis also evidenced a possible difference in the proportion of obese adults between the Americas and Europe on one side and Africa and Asia on the other. Adjustment of the beta regression model with varying dispersion and 5% significance identified mean annual per capita alcohol intake, percentage of insufficient physical activity, percentage of the population living in urban areas, and life expectancy as variables associated with adult obesity.
Keywords:
Obesity; Chronic Disease; Linear Models
Introduction
Adult obesity in the global scenario
Obesity is considered an epidemic disease with major global repercussions, affecting both developed and developing countries 11. Gigante DP, Dias-da-Costa JS, Olinto MTA, Menezes AMB, Silvia M. Obesidade da população adulta de Pelotas, Rio Grande do Sul, Brasil e associação com nível sócio-econômico. Cad Saúde Pública 2006; 22:1873-79.,22. Mariath AB, Grillo LP, Silva RO, Schmitz P, Campos IC, Medina JRP, et al. Obesidade e fatores de risco para o desenvolvimento de doenças crônicas não transmissíveis entre usuários de unidade de alimentação e nutrição. Cad Saúde Pública 2007; 23:897-905.. Causes of obesity can include genetic, metabolic, environmental, social, cultural, economic, lifestyle, and demographic factors 33. Puglia CR. Indicações para o tratamento operatório da obesidade mórbida. Rev Assoc Méd Bras 2004; 50:118.,44. Sichieri R, Moura EC. Análise multinível das variações no índice de massa corporal entre adultos, Brasil, 2006. Rev Saúde Pública 2009; 43 Suppl. 2:90-7..
Body mass index (BMI), which assesses individual fat concentration, is defined as the ratio between body weight in kilograms (kg) and height squared (m2) 55. Linhares RS, Horta BL, Gigante DP, Dias-da-Costa JS, Olinto MTA. Distribuição de obesidade geral e abdominal em adultos de uma cidade no Sul do Brasil. Cad Saúde Pública 2012; 28:438-47.. Persons with BMI ≥ 30kg/m2 are classified as obese.
The World Health Organization (WHO) defines obesity as excessive fat accumulation that presents harm to the person’s health 55. Linhares RS, Horta BL, Gigante DP, Dias-da-Costa JS, Olinto MTA. Distribuição de obesidade geral e abdominal em adultos de uma cidade no Sul do Brasil. Cad Saúde Pública 2012; 28:438-47.. Thus, consumption of energy-dense foods and lack of physical activity are key facilitators of calorie gain and decreased body energy expenditure over the course of the day, making the individual’s energy balance positive and facilitating fat accumulation 66. Carvalho ARM, Belém MO, Oda JY. Sobrepeso e obesidade em alunos de 6-10 anos de escola Estadual de Umuarama/PR. Arq Ciências Saúde UNIPAR 2017; 21:3-12..
Obesity is classified in the group of chronic noncommunicable diseases (NCDs) and is considered one of the most important risk factors for other complications such as diabetes mellitus, hypertension, cardiovascular diseases, etc. 77. Duncan BB, Chor D, Aquino EML, Bensenor IM, Mill JG, Schmidt MI, et al. Doenças crônicas não transmissíveis no Brasil: prioridade para enfrentamento e investigação. Rev Saúde Pública 2012; 46 Suppl 1:126-34.,88. Pinheiro ARO, Freitas SFT, Corso ACT. Uma abordagem epidemiológica da obesidade. Rev Nutr PUCCAMP 2004; 17:523-33.. The NCDs, especially those just cited, pose a serious public health problem as the leading causes of mortality in the world 99. Malta DC, Bernal RTI, Andrade SSCA, Silva MMA, Velasquez-Melendez G. Prevalência e fatores associados com hipertensão arterial autorreferida em adultos brasileiros. Rev Saúde Pública 2017; 51 Suppl 1:11s.. In 2008, for example, NCDs accounted for 63% of deaths in the world, 80% of which in low and middle-income countries 1010. Secretaria de Vigilância em Saúde, Ministério da Saúde. Plano de ações estratégicas para o enfrentamento das doenças crônicas não transmissíveis (DCNT) no Brasil 2011-2022. Brasília: Ministério da Saúde; 2011. (Série B. Textos Básicos de Saúde)..
Obesity is a disease with major social, family, and financial impact, especially for the families of affected individuals. Treatments for obese persons - dealing with the consequences of the condition - represent enormous expenditures for the health system. In Brazil, for example, the costs of procedures associated with overweight and obesity are an estimated 2.1 billion dollars per year 1111. Bahia L, Coutinho ESF, Barufaldi LA, Abreu GA, Malhão TA, Souza CPR, et al. The costs of overweight and obesity-related diseases in the Brazilian public health system: Cross-sectional study. BMC Public Health 2012; 12:440-7.. The United States is one of the countries suffering most from obesity-related problems, since more than a third (35%) of the American population is now obese, and the expenditures for treating the disease exceed billions of dollars a year 1212. Arterburn D, Maciejewski M, Tsevat J. Impact of morbid obesity on medical expenditures in adults. Int J Obes (Lond) 2005; 29:334-9..
The Organisation for Economic Co-operation and Development (OECD) is an international organization consisting of 34 countries - both developed and developing - whose objective is to promote policies that improve the economy and people’s social welfare around the world. The organization’s report for the year 2014 showed that in the previous five years, Canada, England, Italy, Republic of Korea, Spain, and the United States showed modest or practically stable annual growth in overweight and obesity. Meanwhile, Australia, France, Mexico, and Switzerland showed growth of 2% to 3%, with no evidence of a reduction or containment of this epidemic across the countries. It is estimated that countries’ health sector expenditures related to obesity vary from de 1% to 3% and are greater when associated with other complications 1313. Organisation for Economic Co-operation and Development. Obesity update, 2014. http://www.oecd.org/health/Obesity-Update-2014.pdf (acessado em 30/Jun/2017).
http://www.oecd.org/health/Obesity-Updat... .
Therefore, since obesity is a global problem that involves various countries, including Brazil, it is necessary to learn more about the global distribution of obesity and identify possible factors related to its growth in recent years. Several authors have used logistic regression methods for this purpose, particularly in epidemiological studies, in order to identify associations between the independent variables in a context where the response variable is dichotomous and individuals are the unit of interest 1414. Antiporta D, Smeeth L, Gilman RH, Miranda J. Length of urban residence and obesity among within-country rural-to-urban Andean migrants. Public Health Nutr 2015; 19:1270-8.,1515. Shelton N, Knott C. Association between alcohol calorie intake and overweight and obesity in english adults. Am J Public Health 2014; 104:629-31.. The current study aims to examine the distribution of adult obesity across different countries using a beta regression model. This approach is valid since the response variable is a defined proportion on the interval (0,1).
Traditional regression models and the beta regression model
The literature boasts numerous statistical methods that can be used to model data. However, in most cases what one sees is the indiscriminate use of the logistic regression model. It is thus useful to know the different types of models proposed in the literature in order to optimize the analysis of the associations between the independent variables and the response variable.
In various observational or experimental situations, researchers seek to understand and explain phenomena in different areas of science. It is possible to use regression models for this purpose, since they allow expressing the relationship between the response variable Y t and the p independent covariates (X 1 ,…, X p ), addressed in the study. Linear regression is one of the most well-known methods, due to the ease in interpretation of its parameters by researchers, besides being available in various statistical packages. This regression model can be expressed as follows:
With t = 1,…,n, in which n is the total number of observations in the study. Here, Y t is the outcome or response variable, (X 1 ,…,X p ) are the independent covariates, and (β 0 ,…,β p ) are the unknown parameters to be estimated. The errors ε t , are a random, independent sequence with normal distribution with mean zero and constant variance. Briefly, regression models seek to describe the relationship between variables using a mathematical equation 1616. Gurajati DN, Poter DC. Econometria básica. 5ª Ed. Porto Alegre: AMGH Editora; 2011..
Kieschnick & McCullough 1717. Kieschnick R, McCullough B. Regression analysis of variates observed on (0,1): percentages, proportions and fractions. Stat Model 2003; 3:193-213. studied the modeling of variables on the interval (0,1) and identified seven types of models used in the literature to analyze data on the open interval (0,1). These models are: linear normal, logit, censored normal, non-linear normal, beta distribution, simplex distribution, and quasi-likelihood. The authors further discussed the inappropriate use of the ordinary least squares estimator in this setting. Finally, they recommend the use of beta distribution regression or a quasi-likelihood regression 1818. Papke L, Wooldridge J. Econometric methods for fractional response variables with na application to 401(k) plan participation rates. J Appl Econom 1996; 11:619-32. for data with this type of restriction.
Ferrari & Cribari-Neto 1919. Ferrari S, Cribari-Neto F. Beta regression for modeling rates and proportions. J Appl Stat 2004; 31:799-815. proposed the beta regression model to model asymmetrical data on the interval (0,1). This class of models assumes that the distribution of the probability of the response variable is beta, that is, the data must be displayed as rates or proportions, equivalent to prevalence rates in epidemiological models. Unlike linear normal models, the usual estimator is maximum likelihood. It is thus possible to estimate the vector of unknown parameters based on the likelihood function. The normal linear model cannot be used when the data contain zeros and/or ones, that is, when some observation is equal to the interval’s limits. This is because the proportions on the interval (0,1) are not defined on all the real numbers, which is one of the assumptions of normal distribution - the principal characteristic assumed by the variable to allow applying the linear model 2020. Pereira T. Regressão beta inflacionada: Inferência e aplicações [Tese de Doutorado]. Recife: Universidade Federal de Pernambuco; 2010..
In this setting, the beta regression model’s log-likelihood function becomes unlimited. In addition, it is not adequate to assume that the data are from an absolutely continuous distribution. Therefore, an adequate solution would be the zero- or one-inflated beta regression model, in which the response variable’s distribution is a mixture of a Bernoulli distribution and a beta distribution 2020. Pereira T. Regressão beta inflacionada: Inferência e aplicações [Tese de Doutorado]. Recife: Universidade Federal de Pernambuco; 2010..
In the regression structure to model the mean response, the mean response y t is related to a linear predictor η t by means of a link function as follows:
Where β = (β 1 ,…,β k ) T is the vector of unknown parameters to be estimated and X = (X t1 , …,X tk ) are observations of k independent variables. Here, the mean response is obtained by applying the inverse of the link function ɡ(.), that is, µ t = ɡ -1 (𝜂t ).
Importantly, this model assumes a constant precision parameter throughout the observations. Still, in certain situations this parameter may vary over the course of the observations 2121. Almeida Junior P, Souza T. Estimativas de votos da presidente Dilma Roussef nas eleições presidenciais de 2010 sob o âmbito do bolsa família. Ciênc Nat (Impr) 2015; 37:12-22.,2222. Cribari-Neto F, Souza T. Religious belief and intelligence: worldwide evidence. Intelligence 2013; 41:482-9.,2323. Espinheira P, Ferrari S, Cribari-Neto F. Influence diagnostics in beta regression. Computational Statistics & Data Analysis 2008; 52:4417-31.,2424. Espinheira P, Ferrari S, Cribari-Neto F. On beta regression residuals. J Appl Stat 2008; 35:407-19.,2525. Souza S, Oliveira AA, Souza TC, Lima CMBL. Modelagem da proporção de obesos nos Estados Unidos utilizando modelo de regressão beta com dispersão variável. Ciênc Nat (Impr) 2016; 38:1146-56.. That is, the precision parameter is variable and needs to be modeled with a regression structure similar to that of the mean response. The precision’s regression structure is thus defined as:
Where γ = (γ 1 ,…,γ q ) T is a vector of unknown parameters, Z = (Z t1 ,…,Z tq ) are observations of q independent variables (k + q < n), ϑ t is the linear predictor, and h(.) is a link function. There are some possible choices for the link functions ɡ(.)and h(.). For example, for ɡ(.), referring to the model of the mean, one can use the logit link function,
The concept of heteroscedasticity, or non-constant variance of errors, when applied to the beta regression model, differs from that applied to the normal model, which frequently uses variance as a measure of dispersion. In fact, even if the dispersion parameter is constant, the variance of the response variable is non-constant, since it depends on the unknown means that vary according to the model. Dispersion is naturally treated as the inverse of precision, i.e., the greater the dispersion of data over the course of observations, the lesser the precision of the mean response and vice-versa. In addition, the correct modeling of dispersion directly influences the parameters of the mean structure, which improves the inferential results.
Methodology
This is a descriptive ecological study with a quantitative and inferential approach and a focus on regression analysis. The data refer to adult obesity in 78 countries in 2014 in which calculation of the observed proportion was based on the adult population 18 years and older with BMI > 30kg/m2. The sample consisted of 78 observations (proportions) in countries around the world, of which 25 (32%) in Africa, 11 (14%) in the Americas, 14 (18%) in Asia, 25 (32%) in Europe, and 3 (4%) in Oceania.
Data were collected from the online databases of the World Bank (http://databank.wordbank.org) and WHO (http://www.who.int). The World Bank database refers to five institutions that aim to reduce poverty and provide technical and financial assistance to developing countries. The WHO database refers to an organization working in more than 150 countries and relies on governments and other partners to guarantee the highest possible level of health for people.
The collected data were tabulated in an electronic spreadsheet and submitted to the R software (The R Foundation for Statistical Computing; http://www.r-project.org). This software is an open-access platform with various statistical data analysis methods already implemented. Importantly, the most up-to-date available data were collected, covering the largest number of countries. Furthermore, since these are public domain databases, it was not necessary to submit the project to the Institutional Review Board.
Initially, a descriptive analysis of the data was performed to extract important information on the study’s independent variables. The variables cited in this study are listed below with their respective descriptions:
OB2014: proportion of obese adults, 18 years or older, with BMI > 30kg/m2 in 2014;
INAT: percentage of insufficient physical activity in adults in 2010. In other words, the percentage of the target population with less than 150 minutes of moderate physical activity per week or less than 75 minutes of vigorous physical activity per week, or the equivalent;
EDUC: expenditures on education as a percentage of total government spending in 2010;
VIDA: life expectancy at birth (in years) in 2014;
ALC: mean annual per capita consumption of pure alcohol-equivalent, based on the population 15 years and older in 2008;
URB: percentage of the population living in urban areas in 2014.
Next, inferential procedures and goodness-of-fit measures were performed for the beta regression model, using the betareg package of the R software. As discussed, the beta regression model with varying dispersion has the advantage of allowing modeling the data’s variability, which permits improving the inferential results. The model was also chosen because the target variables are furnished as proportions. The beta regression model has the further advantage of allowing expansion of the conclusions concerning the study’s topic by estimating the impact of a given covariable on the mean response.
Results and discussion
Table 1 shows the descriptive data analysis, presenting the minimum value, first quartile (Q 1/4), median, mean, third quartile (Q 3/4), maximum, and coefficient of variation (CV) for the variables used to model the beta regression. From this table, we see that the proportion of obese adults varies from 0.03 to 0.41, with approximately 25% of the 78 countries presenting OB2014 values greater than 0.26 or 26%.
In 50% of the countries, the prevalence of persons practicing insufficient physical activity exceeded 23.8%, with a minimum of 4.10% and maximum of 63.6%. The lowest life expectancy at birth was 49 years and the highest was 83 years, with a mean life expectancy at birth of 72 years. Expenditures on education as a percentage of total government spending varied from 5.53% to 26.3%. Furthermore, 25% of the 78 countries showed EDUC values less than 11.25%. Considering the percentage of the population living in urban areas, 50% of these countries showed values less than 60%, with a minimum of 16.1% and maximum of 100%.
Approximately 25% of the 78 countries showed URB values greater than 74.82%. Mean annual per capita alcohol consumption varied from 0.10 to 15.40 liters, with a mean of 7.39. The CV is defined as the ratio between the standard deviation and the mean, classified as a measure of dispersion. Based on CV, the variable ALC shows the highest variability of data in relation to the mean, with a CV of 0.597. Note that a CV of zero would tell us that the data for a given variable are homogeneous (i.e., all the observations would be equal to the mean).
Colombia, in South America, showed the highest proportion of adults practicing insufficient physical activity. Other countries came close to this proportion, such as Malaysia, South Africa, and Mauritania, the first of which located in Asia and the latter two in Africa. The highest life expectancy values were seen in Spain and Italy, in Europe, followed by Singapore in Asia.
Europe was the continent with the highest per capita alcohol intake. In order, Lithuania, Romania, and Hungary had the highest national alcohol consumption figures in Europe. Singapore and Qatar in Asia and Belgium in Europe were the countries with the highest percentages of people living in urban areas. Africa was the continent with the highest expenditures on education as a percentage of total government spending, led by Ethiopia, Namibia, and Benin. Finally, the highest proportion of obese adults was in Qatar, in Asia, followed by the United States, in North America, while the lowest proportions were in Cambodia and Nepal, in Asia.
As shown in Table 2, OB2014 correlates positively with most of the covariables, except for EDUC. The highest linear correlations with the response variable were for URB and VIDA. Although there was a 0.70 correlation between the two, there were no problems related to the multicollinearity in the further regression analysis.
Figure 1 shows the histogram of frequencies and the boxplot for the variable “proportion of obese adults in 2014”. The figure shows that the response variable’s distribution is asymmetrical, easily observed in the boxplot, since the median is closer to the third quartile. There is also an absence of outliers, or discrepant values outside the boxplot’s limits, which are defined from the quantities Q 1/4 - 1,5 × (Q 3/4 - Q 1/4) and Q 3/4 + 1,5 × (Q 3/4 - Q 1/4), referring to the upper and lower limits, respectively.
Histogram and boxplot for the proportion of obese adults in 78 countries in 2014, respectively.
Figure 2 shows the boxplot for the variable OB2014 on the continents Africa, America, Asia, Europe, and Oceania. The highest concentration of countries with low OB2014 values is in Africa and Asia, while America, Europe, and Oceania have the highest values. Note that there is no intersection between the boxplots for Europe and Oceania and those of Africa and Asia, signifying a possible difference between the proportions of obese adults on these continents.
Boxplot for the variable OB2014 on the continents Africa, the Americas, Asia, Europe, and Oceania.
The beta regression model considered the data set on adult obesity in the countries, totaling 78 observations. Initially, when fitting the beta regression model, it is essential to examine the data’s dispersion. Regression models with varying dispersion require a structure to model the parameters’ precision in order to improve the inferential results 2727. Smithson M, Verkuilen J. A better lemon-squeezer? Maximum likelihood regression with beta-distribuited dependent variables. Psychol Methods 2006; 11:54-71..
The likelihood ratio test was used for this purpose in order to test the null hypothesis of fixed precision, i.e., H 0: (1 = ( = (n = ( 2121. Almeida Junior P, Souza T. Estimativas de votos da presidente Dilma Roussef nas eleições presidenciais de 2010 sob o âmbito do bolsa família. Ciênc Nat (Impr) 2015; 37:12-22.,2525. Souza S, Oliveira AA, Souza TC, Lima CMBL. Modelagem da proporção de obesos nos Estados Unidos utilizando modelo de regressão beta com dispersão variável. Ciênc Nat (Impr) 2016; 38:1146-56.,2828. Neyman J, Pearson E. On the use and interpretation of certain teste criteria for purposes of statistical inference. Biometrika 1928; 20:175-240.. The result was a p-value less than 0.0001 (the value obtained from the sample data reflects the likelihood of rejecting the null hypothesis given that it is true). That is, setting significance at 5%, we reject the null hypothesis of fixed precision. A regression structure is thus necessary to model the data’s precision.
The beta regression model with varying dispersion is as follows:
with t = 1,…,78. In this model, the parameter for precision varies with the observations, thus displaying a heteroscedastic structure. However, even if the data’s dispersion is fixed, the variance of the response variable is non-constant, since the value depends on unknown means that vary with the regression structure.
Table 3 presents the estimates, standard errors, and p-values used to determine the significance of the proposed model’s estimates. Here, the beta regression model with varying dispersion uses the loglog and log link functions to relate the linear predictor to the mean response and the precision, respectively. It is possible to use the Wald test 2929. Wald A. Test of statistical hypotheses concerning several parameters when the number of observations is large. Trans Amer Math Soc 1943; 54:426-82. to verify the null hypothesis that β i = 0 with j = 1,…,p, that is, the variable associated with parameter β i does not present a significant effect on the mean response 3030. Cribari-Neto F, Zeileis A. Beta regression in R. J Stat Softw 2010; 34:1-24.. Thus, considering the 5% nominal level, the variables insufficient physical activity (INAT), persons living in urban areas (URB), alcohol consumption (ALC), and life expectancy (VIDA) are relevant for explaining the proportion of obese adults in countries, since they present p-value < 0.05.
In addition, such covariables show a positive effect by increasing the proportion of obese adults in the countries. That is, the result is consistent with those obtained in the descriptive analysis through the linear correlations with the response variable, presented in Table 2. The positive effect of the INAT variable can be explained by the decrease in the loss of calories over the course of the day due to insufficient physical activity. Meanwhile, the positive effect of the URB variable may be linked to the difficulty in eating meals at home due to growing problems with the urban transportation system caused by increasing urbanization. Thus, the fast pace of modern life encourages the consumption of meals away from home, especially energy-dense “fast foods” 3131. Anjos LA. Obesidade e saúde pública. Rio de Janeiro: Editora Fiocruz; 2006.. Modernization and lifestyle changes due to technological progress also make people more sedentary and increase their odds of becoming obese. The positive effect of the ALC variable can be interpreted as the high calorie intake from alcohol consumption, thereby contributing to the increase in obesity in the countries. Population aging leads to various body changes, with a declining metabolic rate and increase in weight gain 3232. Souza F, Schroeder P, Liberali R. Obesidade e envelhecimento. Revista Brasileira de Nutrição Obesidade e Emagrecimento 2007; 1:24-35..
Thus, the positive effect of the VIDA variable may be related to the aging process, since the higher the life expectancy in the countries, the larger the proportion of elderly individuals.
For example, for countries with the covariables INAT, URB, and ALC fixed on the median and with a life expectancy of 74 years, according to the adjusted model, the estimated mean proportion of obese adults is:
Still, since the link function used was loglog, the inverse function applied to the linear predictor in order to obtain the expected value for the response variable is:
That is, for countries with 23.80% of insufficient physical activity, 60% of the population living in urban areas, mean annual per capita alcohol consumption of 7.15 liters, and life expectancy 74 years, the expected proportion of obese adults is 0.17, or 17%.
As for modeling the precision, Table 3 shows that the covariables life expectancy (VIDA), government spending on education (EDUC), and alcohol consumption (ALC) were statistically relevant at 5% significance. Note that the higher the VIDA and EDUC values in the countries, the lower the data’s precision and thus the greater the dispersion. Meanwhile, the higher the ALC values, the higher the precision, that is, the increase in precision means lower dispersion of the data, making the mean response more precise. In short, modeling the data’s variability is an approach that allows improving the inferential results.
The model’s goodness-of-fit was verified using the adjusted coefficient of determination (pseudo-R2) and the RESET test 3333. Lima L. Um teste de especificação correta para modelos de regressão beta [Dissertação de Mestrado]. Recife: Universidade Federal de Pernambuco; 2007.,3434. Ramsey JB. Tests for specification erros in classical linear least squares regression analysis. J R Stat Soc 1969; 31:350-71.. Pseudo-R2 is a global measure of the explained variation, analogous to the coefficient of determination used in linear regression models. This measure is defined as the square of the sample correlation coefficient between η and ɡ(y) 1919. Ferrari S, Cribari-Neto F. Beta regression for modeling rates and proportions. J Appl Stat 2004; 31:799-815.. Thus, with pseudo-R2 = 0.69, the covariables are said to be capable of explaining about 70% of the total variability in the proportion of obese adults in the countries. In addition, this measure presents values restricted to the interval (0.1), that is, the closer to one, the better the model’s goodness-of-fit or explanatory power.
The RESET test for beta regression models was used to test the model’s correct specification 2121. Almeida Junior P, Souza T. Estimativas de votos da presidente Dilma Roussef nas eleições presidenciais de 2010 sob o âmbito do bolsa família. Ciênc Nat (Impr) 2015; 37:12-22.,2525. Souza S, Oliveira AA, Souza TC, Lima CMBL. Modelagem da proporção de obesos nos Estados Unidos utilizando modelo de regressão beta com dispersão variável. Ciênc Nat (Impr) 2016; 38:1146-56.,3333. Lima L. Um teste de especificação correta para modelos de regressão beta [Dissertação de Mestrado]. Recife: Universidade Federal de Pernambuco; 2007.. The test’s mechanism consists of adding as covariable to the sub-model of the mean the estimated linear predictor raised to the second power, η 2 . The test’s underlying concept is that this covariable has some power to explain the response variable, so we reject the null hypothesis of absence of specification errors. That is, the proposed model presents a correct functional configuration, with no omissions of variables occurring 3434. Ramsey JB. Tests for specification erros in classical linear least squares regression analysis. J R Stat Soc 1969; 31:350-71.. Therefore, with p-value = 0.0075, we lack sufficient evidence to reject the null hypothesis that the model is well specified at 5% level of significance.
Normal probability graph with simulated envelope is a technique that allows identifying deviations from the model’s assumption and possible discrepant observations. Figure 3 shows that the observations are distributed randomly within the envelope’s limits and close to the central line, presenting a reduced number of observations that slightly exceed these limits. Thus, we do not have sufficient evidence to disagree with the model’s adequacy.
It is further possible to estimate a given covariable’s impact, like the percentage of insufficient physical activity on the proportion of obese adults in the countries, as follows 2222. Cribari-Neto F, Souza T. Religious belief and intelligence: worldwide evidence. Intelligence 2013; 41:482-9.:
Where E(.) is the expected value or expectancy. That is, one derives the linear predictor in relation to the target covariable for which one wishes to estimate the individual effect.
Thus, with the aim of estimating the impact curves to describe the effect of insufficient physical activity on the proportion of obese adults in the countries, three situations were considered, as shown in Figure 4, that is, in which the covariables URB, ALC, and VIDA are fixed in the first, second, and third quartiles. It is thus possible to vary the values of INAT to determine the resulting increase in the mean response. As a result, the impact is positive and increases slowly as the levels of insufficient physical activity increase. In addition, there are no major differences between the curves in quantiles 0.50 and 0.75, and they decrease as the INAT values increase. That is, starting at a given value of INAT close to 0.50, no major increases occur in the mean response.
Impact of insufficient physical activity on the proportion of obese adults in 78 countries in 2014.
Final remarks
Given the above, we conclude that 50% of the 78 countries present obesity values greater than 0.20. In addition, their mean life expectancy oscillates around 72 years. Importantly, the levels of insufficient physical activity exceed 23.8% in 50% of the countries. Based on the boxplot analysis, a possible difference was observed in the proportions of obese adults in the Americas and Europe as compared to Africa and Asia.
The beta regression model used here found that the covariables percentage of insufficient physical activity, percentage of the population living in urban areas, life expectancy, and mean annual per capita alcohol intake have a significant and positive effect on obesity. That is, they tend to increase the proportion of obese adults when each of these variables is increased individually while maintaining the others constant.
Acknowledgments
The authors wish to thank the Brazilian National Research Council (CNPq) for the research funding.
References
- 1Gigante DP, Dias-da-Costa JS, Olinto MTA, Menezes AMB, Silvia M. Obesidade da população adulta de Pelotas, Rio Grande do Sul, Brasil e associação com nível sócio-econômico. Cad Saúde Pública 2006; 22:1873-79.
- 2Mariath AB, Grillo LP, Silva RO, Schmitz P, Campos IC, Medina JRP, et al. Obesidade e fatores de risco para o desenvolvimento de doenças crônicas não transmissíveis entre usuários de unidade de alimentação e nutrição. Cad Saúde Pública 2007; 23:897-905.
- 3Puglia CR. Indicações para o tratamento operatório da obesidade mórbida. Rev Assoc Méd Bras 2004; 50:118.
- 4Sichieri R, Moura EC. Análise multinível das variações no índice de massa corporal entre adultos, Brasil, 2006. Rev Saúde Pública 2009; 43 Suppl. 2:90-7.
- 5Linhares RS, Horta BL, Gigante DP, Dias-da-Costa JS, Olinto MTA. Distribuição de obesidade geral e abdominal em adultos de uma cidade no Sul do Brasil. Cad Saúde Pública 2012; 28:438-47.
- 6Carvalho ARM, Belém MO, Oda JY. Sobrepeso e obesidade em alunos de 6-10 anos de escola Estadual de Umuarama/PR. Arq Ciências Saúde UNIPAR 2017; 21:3-12.
- 7Duncan BB, Chor D, Aquino EML, Bensenor IM, Mill JG, Schmidt MI, et al. Doenças crônicas não transmissíveis no Brasil: prioridade para enfrentamento e investigação. Rev Saúde Pública 2012; 46 Suppl 1:126-34.
- 8Pinheiro ARO, Freitas SFT, Corso ACT. Uma abordagem epidemiológica da obesidade. Rev Nutr PUCCAMP 2004; 17:523-33.
- 9Malta DC, Bernal RTI, Andrade SSCA, Silva MMA, Velasquez-Melendez G. Prevalência e fatores associados com hipertensão arterial autorreferida em adultos brasileiros. Rev Saúde Pública 2017; 51 Suppl 1:11s.
- 10Secretaria de Vigilância em Saúde, Ministério da Saúde. Plano de ações estratégicas para o enfrentamento das doenças crônicas não transmissíveis (DCNT) no Brasil 2011-2022. Brasília: Ministério da Saúde; 2011. (Série B. Textos Básicos de Saúde).
- 11Bahia L, Coutinho ESF, Barufaldi LA, Abreu GA, Malhão TA, Souza CPR, et al. The costs of overweight and obesity-related diseases in the Brazilian public health system: Cross-sectional study. BMC Public Health 2012; 12:440-7.
- 12Arterburn D, Maciejewski M, Tsevat J. Impact of morbid obesity on medical expenditures in adults. Int J Obes (Lond) 2005; 29:334-9.
- 13Organisation for Economic Co-operation and Development. Obesity update, 2014. http://www.oecd.org/health/Obesity-Update-2014.pdf (acessado em 30/Jun/2017).
» http://www.oecd.org/health/Obesity-Update-2014.pdf - 14Antiporta D, Smeeth L, Gilman RH, Miranda J. Length of urban residence and obesity among within-country rural-to-urban Andean migrants. Public Health Nutr 2015; 19:1270-8.
- 15Shelton N, Knott C. Association between alcohol calorie intake and overweight and obesity in english adults. Am J Public Health 2014; 104:629-31.
- 16Gurajati DN, Poter DC. Econometria básica. 5ª Ed. Porto Alegre: AMGH Editora; 2011.
- 17Kieschnick R, McCullough B. Regression analysis of variates observed on (0,1): percentages, proportions and fractions. Stat Model 2003; 3:193-213.
- 18Papke L, Wooldridge J. Econometric methods for fractional response variables with na application to 401(k) plan participation rates. J Appl Econom 1996; 11:619-32.
- 19Ferrari S, Cribari-Neto F. Beta regression for modeling rates and proportions. J Appl Stat 2004; 31:799-815.
- 20Pereira T. Regressão beta inflacionada: Inferência e aplicações [Tese de Doutorado]. Recife: Universidade Federal de Pernambuco; 2010.
- 21Almeida Junior P, Souza T. Estimativas de votos da presidente Dilma Roussef nas eleições presidenciais de 2010 sob o âmbito do bolsa família. Ciênc Nat (Impr) 2015; 37:12-22.
- 22Cribari-Neto F, Souza T. Religious belief and intelligence: worldwide evidence. Intelligence 2013; 41:482-9.
- 23Espinheira P, Ferrari S, Cribari-Neto F. Influence diagnostics in beta regression. Computational Statistics & Data Analysis 2008; 52:4417-31.
- 24Espinheira P, Ferrari S, Cribari-Neto F. On beta regression residuals. J Appl Stat 2008; 35:407-19.
- 25Souza S, Oliveira AA, Souza TC, Lima CMBL. Modelagem da proporção de obesos nos Estados Unidos utilizando modelo de regressão beta com dispersão variável. Ciênc Nat (Impr) 2016; 38:1146-56.
- 26McCullagh P, Nelder J. Generalized linear models. London: Chapman and Hall; 1989.
- 27Smithson M, Verkuilen J. A better lemon-squeezer? Maximum likelihood regression with beta-distribuited dependent variables. Psychol Methods 2006; 11:54-71.
- 28Neyman J, Pearson E. On the use and interpretation of certain teste criteria for purposes of statistical inference. Biometrika 1928; 20:175-240.
- 29Wald A. Test of statistical hypotheses concerning several parameters when the number of observations is large. Trans Amer Math Soc 1943; 54:426-82.
- 30Cribari-Neto F, Zeileis A. Beta regression in R. J Stat Softw 2010; 34:1-24.
- 31Anjos LA. Obesidade e saúde pública. Rio de Janeiro: Editora Fiocruz; 2006.
- 32Souza F, Schroeder P, Liberali R. Obesidade e envelhecimento. Revista Brasileira de Nutrição Obesidade e Emagrecimento 2007; 1:24-35.
- 33Lima L. Um teste de especificação correta para modelos de regressão beta [Dissertação de Mestrado]. Recife: Universidade Federal de Pernambuco; 2007.
- 34Ramsey JB. Tests for specification erros in classical linear least squares regression analysis. J R Stat Soc 1969; 31:350-71.
Publication Dates
- Publication in this collection
20 Aug 2018
History
- Received
17 Sept 2017 - Reviewed
13 Mar 2018 - Accepted
23 Mar 2018


 Source: study data, 2016.
Source: study data, 2016. Source: study data, 2016.
Source: study data, 2016.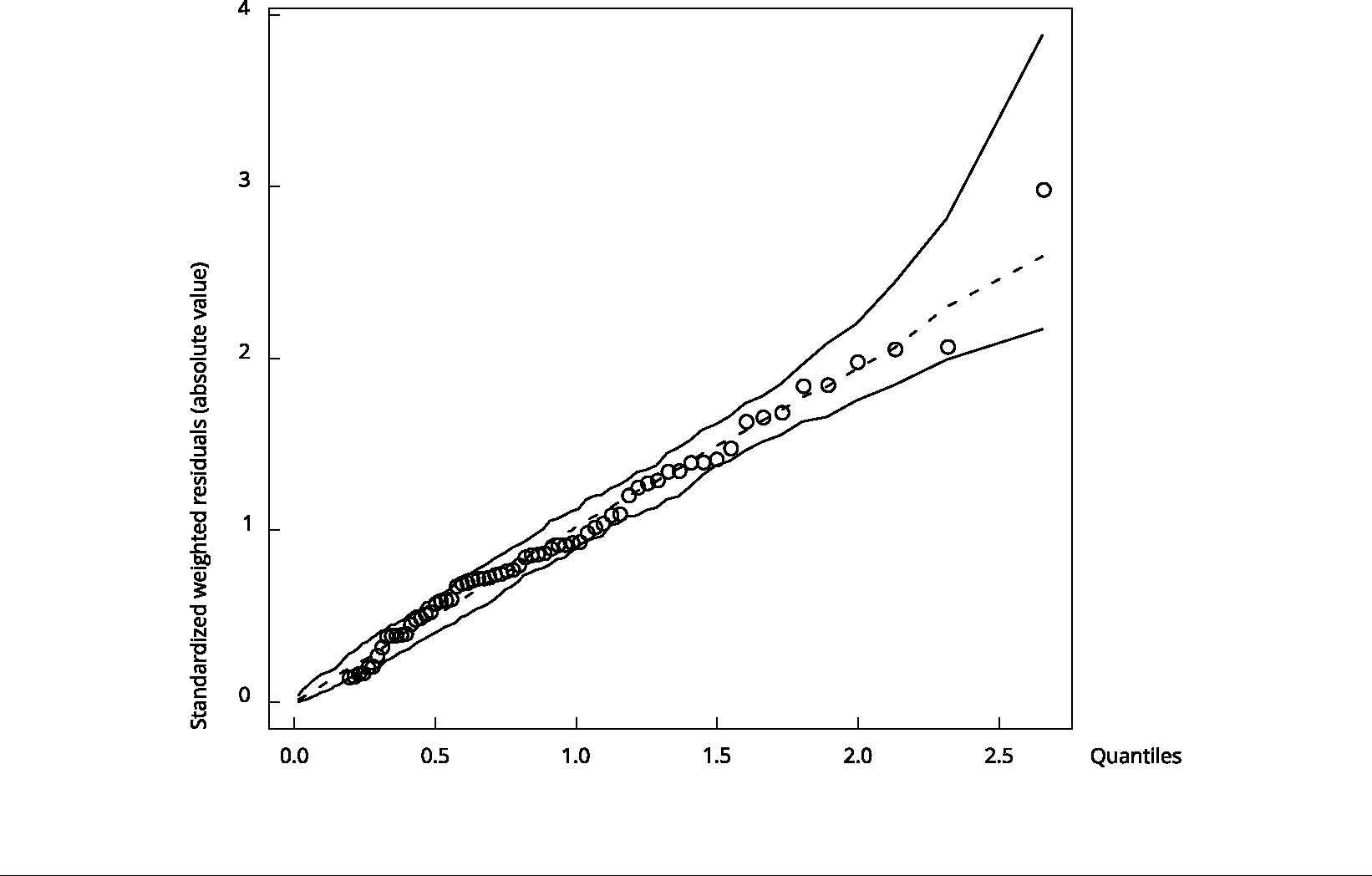 Source: study data, 2016.
Source: study data, 2016. Source: study data, 2016.
Source: study data, 2016.