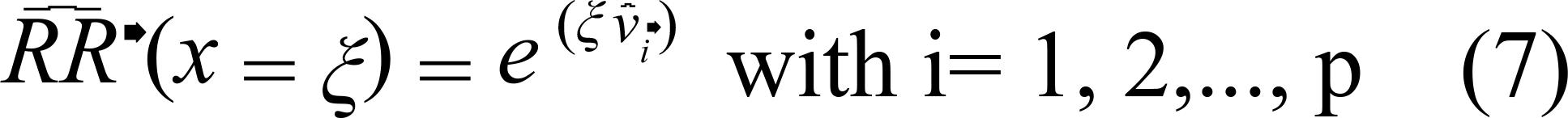Abstracts

INTRODUCTION

The impact of air pollution on human well-being is the main motivation behind its study and control. Air pollution affects the population’s health, even when levels are below those set by legislation.⁶6  Martins L, Latorre MRDO, Saldiva PHN, Braga ALF. Relação entre poluição atmosférica e atendimentos por infecções de vias aéreas superiores no município de São Paulo: avaliação do rodízio de veículos. Rev Bras Epidemiol. 2001;4(3):220-9. DOI:10.1590/S1415-790X2001000300008
https://doi.org/10.1590/S1415-790X200100... Studies have indicated significant associations between daily levels of pollutant concentration and admissions for respiratory or cardiovascular causes,²2  Friedman J. Multivariate adaptive regression splines. Ann Stat. 1991;19(1):1-67.^,44  Johnson RA, Wichern DW. Applied multivariate statistical analysis. 6th ed. New Jersey: Prentice Hall; 2007.^,1010  Wahba G. Splines in nonparametric regression. Encyclopedia of Environmetrics. 2000.^,1111  Wang Y, Pham H. Analyzing the effects of air pollution and mortality by generalized additive models with robust principal components.Int J Syst Assur Eng Manag. 2011;2(3):253-9. DOI:10.1007/s13198-011-0072-7
https://doi.org/10.1007/s13198-011-0072-... among others. The lungs are the main target of air pollution attack, especially in the case of the principal offenders: particulate matter (PM₁₀), sulfur dioxide (SO₂) and (O₃).

Poisson regression with generalized additive models is a statistical tool used to measure and quantify the association between air pollutants and adverse health effects, given the characteristics of the health outcome variable (hospital admission). In this methodology, the co-variables (pollutants) are included in the regression model individually, although the pollutants are co-related. Another alternative is to analyze the principal components of the covariance matrix of pollutants. Evaluating adverse health effects through a combination of pollutants may be easier to interpret and more viable than isolating the effects of one single pollutant. This aspect of the research is current and relevant, and has been previously explored.⁷7  Roberts S, Martin M. Using Supervised Principal Components Analysisto Assess Multiple Pollutant Effects. Environ Health Perspect. 2006;114(12):1977-82.^,1111  Wang Y, Pham H. Analyzing the effects of air pollution and mortality by generalized additive models with robust principal components.Int J Syst Assur Eng Manag. 2011;2(3):253-9. DOI:10.1007/s13198-011-0072-7
https://doi.org/10.1007/s13198-011-0072-... Roberts & Martins⁷7  Roberts S, Martin M. Using Supervised Principal Components Analysisto Assess Multiple Pollutant Effects. Environ Health Perspect. 2006;114(12):1977-82. (2006) evaluated the association of PM₁₀, O₃, SO₂, NO₂ and CO pollutants and their effects on health. The problem of multi-co-linearity (correlation between the pollutants) is solved by principal component analysis (PCA). This is a multiple analysis statistical technique used to reduce dimensionality in a data set while preserving maximum variability of the co-variables,⁴4  Johnson RA, Wichern DW. Applied multivariate statistical analysis. 6th ed. New Jersey: Prentice Hall; 2007. allowing pollutants to be grouped into a regression model. The authors suggest a descriptive method of “supervised PCA”, in which the relationship between the co-variables (pollutants) and effects harmful to health are observed before being included in the regression model. The effect of the joint association of the pollutants on daily mortality was analyzed by Wang & Pham¹¹11  Wang Y, Pham H. Analyzing the effects of air pollution and mortality by generalized additive models with robust principal components.Int J Syst Assur Eng Manag. 2011;2(3):253-9. DOI:10.1007/s13198-011-0072-7
https://doi.org/10.1007/s13198-011-0072-... (2011), using the PCA and a robust method. The results show more expressive estimates of relative risk (RR) when applied to the PCA multiple analysis technique, evidencing stronger associations between the variables.

Using the PCA requires data obtained through independent replications. However, when using them to make statistical inferences, due attention needs to be paid to co-variables correlated in time, such as air pollutants.

Statistical stationarity must be satisfied. The principal components are linear combinations of the co-variables, the properties of which are transferred linearly to the components.

The effect of the correlations on the inferential context has been studied by Zamprogno^aa Zamprogno B. Análise de componentes principais no domínio do tempo e suas implicações em dados autocorrelacionados [doctoral thesis]. Vitória: Programa de Pós-Graduação em Engenharia Ambiental do Centro Tecnológico da UFES; 2013. and theoretically and empirically shows the temporal correlation effect of the co-variables when this procedure is neglected. In proposition 1, the author shows that the components are temporally correlated. PCA in regression should be used with caution, as it bears the temporal structure of the variables.

The aim of this study was to analyze the association between concentrations of air pollutants and daily hospital admissions of children for respiratory causes.

METHODS

This was an ecological time series study. The hospital admissions of 59,353 children aged < 6 in Grande Vitória, ES, between January 1, 2005 and December 31, 2010, were analyzed. Data were obtained from the Hospital Infantil Nossa Senhora da Glória children’s hospital (HINSG) records, where the main children’s emergency room for the Grande Vitória region is based. Respiratory disease was classified according to the International Classification of Diseases (ICD-10) categories.

Data on daily pollutant levels – particulate matter (PM₁₀), sulfur dioxide (SO₂), nitrogen monoxide (NO₂), ozone (O₃) and carbon monoxide (CO) – and the meteorological variables were obtained from the Instituto Estadual de Meio Ambiente e Recursos Hídricos (IEMA – State Institute for the Environment and Water Resources), measured and collected at eight monitoring stations from the air quality automatic monitoring network (RAMQAr).

The data collection included the 24h period for all of the pollutants and began in the first half hour of the day. The 24h mean for PM₁₀ and SO₂ and 8h moving average for CO and O₃ were considered, as was the 24h maximum for NO₂ from each station. The daily mean of the variables from all the stations were the co-variables used in the generalized additive model (GAM) and its extension, the GAM-PCA. The atmospheric variables were measured in μg/m³3  Gouveia N, Bremner SA, Novaes HM. Association between ambient air pollution and birth weight in São Paulo, Brazil. J Epidemiol Community Health. 2004;58(1):11-7. DOI:10.1136/jech.58.1.11
https://doi.org/10.1136/jech.58.1.11... and the meteorological variables (temperature and relative humidity) measured in their units (ºC and %, respectively).

The variables in question were modelled using time series, regression models and multiple analysis techniques. The aspects of the GAM enabled parametric and non-parametric functions in adjusting the mean data curve. The outcome was modelled assuming that the basic distribution of the number of health events (hospital admissions) followed Poisson distribution. The daily number of admissions for respiratory disease was the dependent variable, and the daily concentrations of air pollutants the independent variables. A common characteristic of the variables was missing observations, either due to incorrect measurements, equipment failure or invalid measurements, among others. These variables were adjusted using imputation, as described by Junger,^bb Junger WL. Análise, Imputação de dados e interfaces computacionais em estudos de séries temporais epidemiológicas [doctoral thesis]. Universidade Estadual do Rio de Janeiro; 2008. in which the estimates are obtained using spatial correlation between the levels of pollutant and by autocorrecting of the levels of this pollutant.

The models were analyzed and adjusted in stages. Seasonality was of short duration with indicator variables for days of the week and holidays. The “loess” smoothing function²2  Friedman J. Multivariate adaptive regression splines. Ann Stat. 1991;19(1):1-67. was used for long-term seasonality. This enables non-linear dependence between the variables in question (admissions) and seasonality to be controlled. The confounding co-variables (temperature and relative humidity) were modelled using smoothing “splines”.²2  Friedman J. Multivariate adaptive regression splines. Ann Stat. 1991;19(1):1-67.^,1010  Wahba G. Splines in nonparametric regression. Encyclopedia of Environmetrics. 2000. The principal components were calculated using a covariance matrix of the pollutants in question.

PCA multiple analysis was used to evaluate the joint effects of the pollutants, eliminating correlation between them and the simultaneous effect of the pollutants was investigated. The regression model used was the GAM and its extension, the GAM-PCA. The effects of pollution on health were calculated using RR, which expresses the probability of an individual developing a disease relative to exposure to a risk factor. The RR estimate was used to compare the proposed models,

RR was obtained by solving a system of equations from the GAM model and applying PCA. The results consider the interquartile variations of the pollutants and were calculated by %RR = (RR - 1)*100.

GAM¹³ with marginal Poisson distribution is usually reported in analyzing the association between the outcome variable and the explanatory co-variables. It is widely used as non-linear modelling describes the relationship between the variables in question.¹1  Chen R, Chu C, Tan J, Cao J, Song W, Xu X, et al. Ambient air pollution and hospital admission in Shanghai, China. J Hazard Mater. 2010;181(1-3):234-40.^,22  Friedman J. Multivariate adaptive regression splines. Ann Stat. 1991;19(1):1-67.^,88  Freitas C, Bremner SA, Gouveia N, Pereira LAA, Saldiva PHN. Internações e óbitos e sua relação com a poluição atmosférica em São Paulo, 1993 a 1997. Rev Saude Publica. 2004;38(6):751-7. DOI:10.1590/S0034-89102004000600001
https://doi.org/10.1590/S0034-8910200400... ^,99  Schwartz J. Harvesting and long term exposure effects in the relationship between air pollution and mortality. Am J Epidemiol. 2000;151(5):440-8.

When {Y_t}, t = 1,..., N, a time series count formed of non-negative integers. The conditional density of {Y_t} given Ƒ_t-1, shown by Y_t / Ƒ_t-1, possesses Poisson distribution, with a mean µ_t , the following equation is satisfied:

when

The vector of dimension p of the co-variables which can include previous values Y_t as well as other auxiliary data, such as the pollutants, confounding variables (trends, seasonality and meteorological variables among others).⁵5  Kedem B, Fokianos K. Regression models for time series analysis. 2th ed. Hoboken: Wiley; 2002. DOI:10.1002/0471266981
https://doi.org/10.1002/0471266981...

The curve which describes the relationship between Y_t and X, the co-variance vector, is obtained by the logarithmic transformation of µ_t :

When β_j is the vector of the coefficients to be estimated (co-variables) and ƒ(x_j) are the smoothing functions for the confounding variables (temperature and humidity) and long-term seasonality present in the data. β₀ corresponds to the intercept of the curve associated with the vector of unitary values.

RR is a measure often used in epidemiological studies to measure the impact of the concentration of air pollutants on the health of the exposed population. RR can be defined as the relationship of the probability of an event occurring after certain exposure to a risk factor, in the case of this study, exposure to concentrated levels of air pollutants. In the case of the GAM model with marginal Poisson distribution, RR(x) is estimated using the following formula:¹²12  Zou G. A modified poisson regression approach to prospective studies with binary data. Am J Epidemiol. 2004;159(7):702-6. DOI:10.1093/aje/kwh09
https://doi.org/10.1093/aje/kwh09...

In which ξ is the variation in the concentrations of the pollutant which can, for example, assume the value 10 µg/m³, of the interquartile variation, among others, and is the estimated coefficient associated with the pollutant being studied. When the level of significance is α, the hypothesis to be tested is defined as H₀: RR(x) = 1 against H₁: RR(x) > 1. Not rejecting H₀ statistically implies that the pollutant studied does not adversely affect health.

PCA is a statistical multi-analysis technique that aims to reduce the dimensionality of the data’s matrix space by linear transformation of the original variables. Correlation between the variables implies multi-colinearity is occurring in the regression models. In this article, the PCA technique was used to solve a problem of correlation between the pollutants, the variability of the system as determined by k variables can only be explained for k principal components. However, a large part of this variability may be explained by a lower r number of components, r ≤ k.⁴4  Johnson RA, Wichern DW. Applied multivariate statistical analysis. 6th ed. New Jersey: Prentice Hall; 2007.

When (λ₁, α₁), (λ₂, α₂), ... , (λ_k, α_k) the eigenvalues-eigenvectors pairs, respectively, of the Σ matrix of covariance of the X vector. The i-th principal component of Σ is given by

The co-variables produced by applying PCA, defined here as PC, are linear combinations of the original environmental variables. Including new co-variables in the GA < model is defined using the following formula:

In which ν_i is the estimated vector of the principal components (PC) and ƒ(x_i) are the smoothing functions for the confounding variables (temperature and humidity). The estimated RR for model 6 is given by:

In which ξ is the variation in concentration of the pollutant given by the interquartile variation. is represented by the expression:

in which α_ij corresponds to the associated auto vectors of the co-variables j;  is the estimated coefficient of the i-th principal component and  is easily obtained using equations 5 and 6.

The 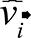coefficient is obtained with a linear solution of equations 5 and 6, in which the individual contribution of each pollutant is extracted from the linear combination of all pollutants (equation 5) using equation 6.

RESULTS

The mean number of daily admissions was 27.1, SD 18.1 (Table 1).

The meteorological variables (temperature and relative humidity) were from the Carapina monitoring station. The mean maximum temperature used in the model was 29.4ºC (SD = 3.3ºC) and mean relative air humidity was 77.4% (SD = 6.0%).

There was an indication of moderate and weak correlation between the air pollutants (Table 2).

The first three components explained 83.2% of total variability in the variables. The proportion of accumulated variability was used as a criterion when choosing the components in the GAM. Similar results in the modelling were found when the first four components were used. It was decided to use the first three using the criterion of parsimony as co-variables and they are shown in bold (Table 3).

The highest coefficients (auto vectors) of components 1, 2 and 3 were from CO, O₃ and SO₂, respectively. It was suggested to divide the clusters by each component grouped, e.g., pollutants with factorial loads > 0.5. Such suggestions are indicated by (*) for each principal component (Table 3).

An autoregressive seasonal model of the moving average (SARMA) (1,0,0)(1,0,0)₇ was adjusted for the residuals of the GAM-PCA, resulting in the GAM-PCA-SAR final model. This eliminated auto-correlation of the data.

Comparative study of the quality of fit of the two proposed models was conducted using  , defined as:

In which with being the predictive value of Y_i the number of hospital admissions, the GAM results were approximately 35.0% higher than those obtained by the GAM-PCA.

RR values for each pollutant and model were calculated in order to compare the performance of the GAM and GAM-PCA-SAR adjusted models in the variables. The results were expressed by interquartile variation increment, once the RR analysis was conducted for pollutants of different scales (Table 4). The estimated RR results were significant for all models. The most significant estimated RR models were obtained principally through the proposed GAM-PCA model.

RR estimates for PM₁₀ increased from approximately 2.0% to 3.0% . Significant increases in estimated RR values were observed for CO. In this case, . Thus, the proposed GAM-PCA-SAR model shows more significant results in the expected increase in the number of admissions for respiratory causes, compared with the usual GAM.

DISCUSSION

This article proposes the use of two statistical techniques aiming to improve the performance of the model of association between air pollutants and hospital admissions for respiratory disease. It was verified that the RR estimates were better in general levels of analysis, especially when compared with the models usually used in the literature. The PCA technique eliminates correlation between the pollutants studied.

The model proposed in this study is denominated the GAM-PCA, and uses the principal components of the original data as co-variables in the GAM model. As there is auto-correlation in these components, this property is transferred to the residuals of the adjusted GAM-PCA model. The residuals of this model were adjusted using the autoregressive integrated seasonal model of the moving average (SARIMA) (1,0,0)(1,0,0)₇. The final model was defined as GAM-PCA-SAR, with the use of the SAR model, particular case of the SARIMA model.

The quality of fit of the dominated models was calculated using estimated mean squared error (MSE). The results indicate that the MSE of the usual GAM model was 35.0% higher than that of the proposed GAM-PCA-SAR model, in other words, the proposed model showed better results than that usually used in the literature.

The levels of concentration of pollutants studied did not exceed the primary standard of air quality recommended by the National Environmental Council (CONAMA),^cc Ministério do Meio Ambiente. Conselho Nacional do Meio Ambiente. Resolução CONAMA nº 003, de 28 de junho de 1990. Dispõe sobre o estabelecimento de padrões nacionais de qualidade do ar determinando as concentrações de poluentes atmosféricos. Diario Oficial Uniao. 22 ago 1990 [2013 Oct 21] Seção1:15937-9. Available from: http://www.mma.gov.br/port/conama/legiabre.cfm?codlegi=100 or the limits set by the World Health Organization (WHO).^dd World Healthy Organization. WHO Air quality guidelines for particulate matter, ozone, nitrogen dioxide and sulfur dioxide. Global update 2005. Genebra; 2006. However, other studies have shown that pollutants can have harmful effects on human health, even at levels of exposure below the levels set as acceptable.^aa Zamprogno B. Análise de componentes principais no domínio do tempo e suas implicações em dados autocorrelacionados [doctoral thesis]. Vitória: Programa de Pós-Graduação em Engenharia Ambiental do Centro Tecnológico da UFES; 2013.

Harmful effects on the health of children in the Grande Vitória region from exposure to concentrations of pollutants were obtained by estimating Relative Risk in the proposed regression models GAM, GAM-PCA-SAR.

Based on the theoretical and empirical studies presented by Zamprogno,^aa Zamprogno B. Análise de componentes principais no domínio do tempo e suas implicações em dados autocorrelacionados [doctoral thesis]. Vitória: Programa de Pós-Graduação em Engenharia Ambiental do Centro Tecnológico da UFES; 2013. the PCA technique can be applied without leading to spurious interpretations and tests when the auto-correlation of the process is weak.

Descriptive and graphic analyses motivated the use of the PCA technique with the data on air pollutants, even with the indication that the correlation and auto-correlation of the pollutants is weak.

An increase of 10.5 μg/m³ (interquartile interval) in the levels of particulate material (PM₁₀) lead to for 1.029 (95%CI 0.991;1.09) in the GAM-PCA-SAR model. Similar interpretations can be observed for other pollutants in the usual GAM. The results found in this study using GAM and GAM-PCA corroborate those found in studies conducted by Roberts & Martins⁷7  Roberts S, Martin M. Using Supervised Principal Components Analysisto Assess Multiple Pollutant Effects. Environ Health Perspect. 2006;114(12):1977-82. (2006). The authors consider the relationship between morbidity and concentrations of air pollutants for data recorded in Korea. The article proves that using PCA improves estimates of relative risk.

The results of this study indicate the significant relationship between concentrations of levels of pollutants and the number of hospital admissions in children aged < 6, even in environments where levels are below the limits recommended by CONAMA^cc Ministério do Meio Ambiente. Conselho Nacional do Meio Ambiente. Resolução CONAMA nº 003, de 28 de junho de 1990. Dispõe sobre o estabelecimento de padrões nacionais de qualidade do ar determinando as concentrações de poluentes atmosféricos. Diario Oficial Uniao. 22 ago 1990 [2013 Oct 21] Seção1:15937-9. Available from: http://www.mma.gov.br/port/conama/legiabre.cfm?codlegi=100 and the WHO.^dd World Healthy Organization. WHO Air quality guidelines for particulate matter, ozone, nitrogen dioxide and sulfur dioxide. Global update 2005. Genebra; 2006. The principal components obtained using the variance/co-variance matrix applied to the processes indexed in time show temporal correlation. It is proposed that parametric filters be used with the original variables in order to remove temporal correlation. The filtering method, using the vector auto regression (VAR) model, is suggested as an alternative procedure for transforming atmospheric data in a white noise process.

It is recommended that the PCA technique be used to analyze frequency data, and that other susceptible population groups should be studied, as well as other types of disease, such as cardiovascular disease. Other techniques could be used, such as the bootstrap technique, to estimate confidence intervals with more precision, and that of generalized linear autoregressive moving average (GLARMA) modelling, to resolve the problem of serial auto-correlation of the data.

ACKNOWLEDGEMENTS

Thanks to the Instituto Estadual de Meio Ambiente (IEMA) and to the Hospital Infantil Nossa Senhora da Gloria (HINSG), for providing environmental and hospital data, respectively.

REFERENCES

Publication Dates

History